Question 515226: The perimeter of a rectangle is 86m. If the width were doubled and the length were increased by 22m, the perimeter would be 166m. What are the length and width of the rectangle?
I appreciate any help......
Answer by drcole(72)   (Show Source):
You can put this solution on YOUR website! Let W be the original width and let L be the original length. The perimeter of the original rectangle is going to be the sum of twice the width and twice the length, or algebraically 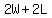 . We know that the original perimeter is 86 meters, so we have the equation:
Doubling the width would give us a width of 2W, and increasing the length by 22 meters would give us a length of L + 22. The new perimeter is also the sum of twice the (new) width and twice the (new) length, which algebraically is  . The new perimeter is 166 meters, so this fact gives us the equation
 (distributing the two 2s on the left hand side)
 (subtracting 44 from both sides)
We now have two linear equations in two unknowns. We notice that both equations contain 2L in them, so if we subtract the first equation from the second, we can eliminate the variable L and just solve for W. This is the elimination method.
 (subtracting the first equation from the second, or more specifically, subtracting 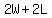 from the left hand side of the second equation, and 86 from the right hand side)
 (dividing both sides by 2)
So W = 18. Substituting 18 for W into the first equation, we get an equation for L alone:
 (substituting 18 for W in the first equation)
 (simplifying the left hand side)
 (subtracting 36 from both sides)
 (dividing both sides by 2)
So we have that the original width is 18 meters, and the original length is 25 meters. Let's check if these numbers work: for the original rectangle, these measurements would give a perimeter of 18 + 18 + 25 + 25 = 86 meters, which is what we want. For the new rectangle, the width is doubled to 36 meters, and the length is increased by 22 meters, to 47 meters. This gives a perimeter of 36 + 36 + 47 + 47 = 166 meters, which is also what we wanted, so our answer is correct.
|
|
|
