Question 515185: Find the LCM of (9+7r), (81-49r^2), and (9-7r)
Thanks,
Dee
Answer by drcole(72)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the least common multiple, we need to first factor each of the expressions. The first,  , and the third, , and the third,  , cannot be factored, but the second, , cannot be factored, but the second,  , is the difference of two squares: , is the difference of two squares:
 and and 
Remembering that every difference of two squares 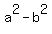 can be factored as: can be factored as:

we get that

So we are trying to find the least common multiple of  , , 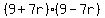 , and , and  . The least common multiple of three expressions A, B, and C is the simplest expression that contains A, B, and C in its factorization. So the least common multiple has to contain at least one . The least common multiple of three expressions A, B, and C is the simplest expression that contains A, B, and C in its factorization. So the least common multiple has to contain at least one  and one and one  in its factorization, since those appear in A and C. Do we need anything else? No, because in its factorization, since those appear in A and C. Do we need anything else? No, because  , so , so  doesn't add any new factors to the least common multiple. So the least common multiple must be doesn't add any new factors to the least common multiple. So the least common multiple must be 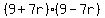 or or  . .
|
|
|