Question 515104: An equation relating the number N of atoms of radium at any time, t, in terms of the number N0 of atoms, at t =0, is loge(N/N0) = -kt, where k is a constant. Solve for N.
Answer by drcole(72)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are given the equation:

First, it is customary to write 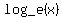 as as 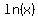 . .

The logarithm base e of a number is called the natural logarithm of the number. The constant e is a very special number that shows up in nature and finance all of the time, and is approximately equal to 2.718.
Now, the important thing to understand about all logarithms is that they are the inverse functions of exponentiation. In other words, suppose we start with a number x, and we take the logarithm base a of x: 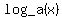 . To get back to x, we raise a to the power of the logarithm we just took: . To get back to x, we raise a to the power of the logarithm we just took:

Exponentiation and logarithms are inverses just like squaring and square roots are inverses: if you take the square root of x, and then square the square root you just got, you get back x:

In your problem, you want to solve for N, but N is inside of a natural logarithm (a logarithm base e). We want to get rid of that natural logarithm, so we raise the number e to the power of the left hand side of the equation. Of course, if we do something to the left side, we have to also do it to the right side, and this is what we get:
 (exponentiating both sides using e) (exponentiating both sides using e)
 (simplifying the left side, since exponentiation and logarithms are inverses) (simplifying the left side, since exponentiation and logarithms are inverses)
Isolating N is now simple:
 (multiply both sides by (multiply both sides by  ) )
So now we have a formula for the number of atoms of radium at time t.
|
|
|