SOLUTION: Write the complex number z=-4-5i in trigonometric form (sometimes called polar form), with the angle expressed in radians from 0 to 2pi. Do not round any intermediate computations,

We want it in the form -4-5i = R(cos + i*sin)


First let's draw the complex number -4-5i. It is the vector drawn from 
(0,0) to the point (-4,-5).  Here it is (in green):



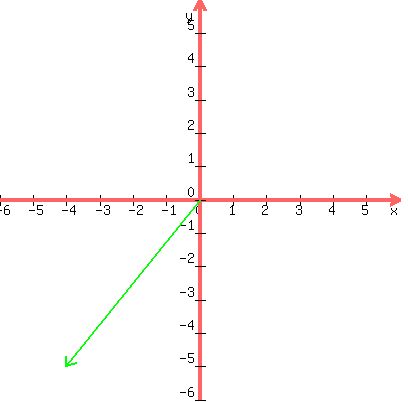Now let's draw a vertical line from the tip of the
vector z to the x-axis  (in blue):


 
So we have x = -4, y = -5



We calculate R from R = 



Now that we have R, we only need to find , which is the
angle marked  below and indicated by the red arc, rotating
from the right side of the x-axis counter-clockwise around to the 
green vector. 



However the calculator will not give us that value for .
So we get the reference angle, which is indicated by the blue arc
below:



Now we use our calculator to find the inverse tangent of , and

find the angle indicated by the blue are (called the "reference angle"
 to be 0.8960553846 radians.

However we must add  to that number to indicate the complete
angle .  So we have  =  + 0.8960553846
= 4.037648038, which rounds to 4.04 radians.  Therefore the 

-4-5i = R(cos + i*sin) = (cos4.04 + i*sin4.04).  You can also evaluate  as 6.403124237
and make the answer 

6.40(cos4.04 + i*sin4.04)

Edwin