Question 514864: A 10m by 20m pool is surrounded by a deck of uniform width. The area of the deck is 216m^2. How wide is the deck?
Answer by drcole(72)   (Show Source):
You can put this solution on YOUR website! Try drawing a picture. Let x represent the width of the deck. We can break the deck up into eight pieces: the two rectangles adjacent to the long sides of the pool, the two rectangles adjacent to the short sides of the pool, and the four corners, each of which is a square with sides the width of the deck. Let's describe the areas of each piece of the deck algebraically:
Each rectangle adjacent to a long side of the pool has length 20 meters and width x meters, and thus area 20x square meters.
Each rectangle adjacent to a short side of the pool has length 10 meters and width x meters, and thus area 10x square meters.
Each square corner has all sides of width x meters, and thus has area x^2 square meters.
Since there are two of each rectangle and four square corners, the total area of the deck is:
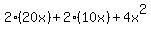
We know that the area of the deck is 216 square meters, so we have a quadratic equation we can solve:
Now we solve:
 (simplify the left hand side)
 (combine like terms)
 (subtract 216 from both sides and rearrange terms)
 (divide both sides by 4)
 (factor the quadratic: 18 and -3 have a sum of 15 and a product of -54)
Setting both factors equal to 0, we get the roots x = -18 and x = 3. Now x = -18 cannot be the solution, since x represents a width and cannot be negative. So the only realistic solution is x = 3. So the deck has a uniform width of 3 meters.
|
|
|
