SOLUTION: One number is 5 more than another. Five times the smaller is 2 more than twice the larger. Find the numbers. Bill has twice as much money as bob. Paul has $12 more than Bill.

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: One number is 5 more than another. Five times the smaller is 2 more than twice the larger. Find the numbers. Bill has twice as much money as bob. Paul has $12 more than Bill.       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 51422: One number is 5 more than another. Five times the smaller is 2 more
than twice the larger. Find the numbers.
Bill has twice as much money as bob. Paul has $12 more than Bill.
Together they have $92. How much money does Bob have?
Find two consecutive whole numbers that total 93.
WORK DONE :
NOTHING IM COMPLETELY LOST!!!!!!!
I do not remmeber what to do.

Answer by rchill(405) About Me  (Show Source):
You can put this solution on YOUR website!
You have three separate problems here -- you should probably ask one problem at a time in the future.


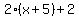In the first problem we're told that one number is 5 more than another. Let x represent the number, then x%2B5 represents the other. Five times the smaller (i.e., 5x) is 2 more than twice the larger (i.e., 2%28x%2B5%29%2B2). This produces the equation 5x=2%28x%2B5%29%2B2. Now we just solve for x. Expanding the equation produces 5x=2x%2B10%2B2 which simplifies to 5x=2x%2B12. Subtracting 2x from both sides produces 3x=12. Now divide both sides by 3 yields x=4. This means the smaller number is 4 and the other number is 5 more than that; i.e. 4+5, or 9.


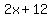For the second problem, let x represent the money for Bob. Bill has twice that amount, or 2x. Paul has $12 more than Bill, or 2x%2B12. Together they have $92, represented by the equation x%2B2x%2B2x%2B12=92. We combine like terms to get 5x%2B12=92. Subtracting 12 from both sides yields 5x=80. Now divide both sides by 5 to produce x=16. That means Bob has $16. Bill has twice that, or $32; Paul has $12 more than Bill, or $44. Adding $16+$32+$44 produces the sum of $92.


For the third problem, let x represent one of the numbers. Because the numbers are consecutive, the other number is represented by x%2B1. Their sum must total 93, represented by the equation x%2Bx%2B1=93. Combining like terms produces 2x%2B1=93. Solving for x as in the process above produces x=46. That means the second number is one more than that, or 47. Sure enough, 46%2B47=93.