SOLUTION: Barry can do a certain job in 10 hours, whereas it takes Samuel 12 hours to do the same job. How long would it take them to do the job working together?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Barry can do a certain job in 10 hours, whereas it takes Samuel 12 hours to do the same job. How long would it take them to do the job working together?       Log On


   

Question 514070: Barry can do a certain job in 10 hours, whereas it takes Samuel 12 hours to do the same job. How long would it take them to do the job working together?
Answer by drcole(72) About Me  (Show Source):
You can put this solution on YOUR website!
We'll assume that Barry and Samuel complete their jobs at a constant pace. If Barry can do this job in 10 hours, then he can do 1%2F10 of a job in 1 hour. Likewise, if Samuel can takes 12 hours to do the same job, he can do 1%2F12 of a job in 1 hour. In both cases, we took the reciprocal to go from hours per job to job per hour. So together,

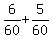
+6%2F60+%2B+5%2F60+
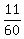+11%2F60+ (putting both fractions over the least common denominator of 10 and 12, which is 60, and adding)
Thus together, Barry and Samuel complete 11/60 of a job in one hour. The number of hours it takes to complete the job will be the reciprocal of this fraction: it takes 60/11 of a hour, or 5 5/11 hours, to Barry and Samuel to complete the job together. We're taking the reciprocal because we are going from jobs per hour to hours per job.