SOLUTION: Evaluate : 1+ (1+2) +(1+2+3) + (1+2+3+4) +............(1+2+.....100)

1 + (1+2) + (1+2+3) + (1+2+3+4) + ··· + (1+2+···+100)

I'll get one more term:

1 + (1+2) + (1+2+3) + (1+2+3+4) + (1+2+3+4+5) + ··· + (1+2+···+100)

1 + 3 + 6 + 10 + 15 + ··· + (1+2+···+100)

n   an  Sn  d1   d2  d3
1   1   1   1   2   1
2   3   4   3   3   
3   6  10   6      
4  10  20     
5  15     
  

It takes three differences to get a constant column, so
we will assume a quadratic sum formula Sn

Sn = An³ + Bn² + Cn + D

S1 = A(1)³ + B(1)² + Cn + D

1 = A + B + C + D

S2 = A(2)³ + B(2)² + C(2) + D

4 = A(8) + B(4) + 2C + D

4 = 8A + 4B + 2C + D

S3 = A(3)³ + B(3)² + C(3) + D

10 = A(27) + 9B + 3C + D

10 = 27A + 9B + 3C + D

S4 = A(4)³ + B(4)² + C(4) + D

20 = A(64) + 16B + 4C + D

20 = 64A + 16B + 4C + D

So we have the system of equations:

 1 =   A +   B +  C + D
 4 =  8A +  4B + 2C + D
10 = 27A +  9B + 3C + D
20 = 64A + 16B + 4C + D

or in standard order:

  A +   B +  C + D =  1
 8A +  4B + 2C + D =  4
27A +  9B + 3C + D = 10
64A + 16B + 4C + D = 20

Solve that system and get

A = , B = , C = , D = 0

Then this

Sn = An³ + Bn² + Cn + D

becomes

Sn = n³ + n² + n + D

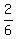Sn = n³ + n² + n + D

Sn = 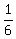(n³+3n²+2n)

Sn = 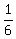n(n²+3n+2)

Sn = 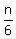(n+1)(n+2)

That's the general formula, so the sum of the first 100 terms is
found by substituting n = 100:

S100 = 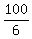(100+1)(100+2)

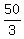S100 = (101)(102)

S100 = 171700

Edwin