7x³ - 6x² + 2x - 1 = 0
Every candidate for a rational solution is ± a fraction whose
numerator is a divisor of the absolute value of the constant term,
-1, and whose denominator is a divisor of the absolute value of the
leading coefficient, 7.
The only divisor of |-1| is 1
The only divisors of |7| are 1 and 7
Therefore the only candidates for rational solutions are
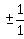and 
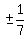. The only ones of those which
are integers are 1 and -1, so we see if either of those is a
solution:
We see if 1 is a solution using synthetic division:
1| 7 -6 2 -1
| 7 1 3
7 1 3 2
That left a remainder of 2, not 0, so 1 is not a solution
We also see if -1 is a solution
-1| 7 -6 2 -1
| -7 13 -15
7 -13 15 -16
That left a remainder of -16, not 0, so -1 is not a solution
either.
Those two, 1 and -1, were the only possible candidates for integer
solutions. So there are none.
Edwin
