Question 510981: Solve for X:
 + + 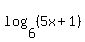 = = 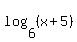 +1 +1
And we were asked to find it without a calculator.
Being all log base 6, I originally tried to thus make it 5(5x+1)=(x+5)+1. Which would be (25x+5)=(x+6). I then subtracted x and 5 from both sides, getting (24x)=1. Divided by 24 to get x by itself, and I got x=(1/24). However, that was not one of the answers. The answers were along the lines of -19/24, 19/24, 24/19, -24/19. (Can't entirely recall what the exact options were, but those were close)
Anyway, if you could explain how to do this, that would be great, opposed to just answering the question. ^^ Or show a step by step or something, so I can understand how to do this in future problems. Please solve without calculator use ^^
~ Thanks
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! --------------
log(5)/log(6) + log(5x+1)/log(6) = log(x+5)/log(6) + 1
----
Multiply thru by log(6) to get:
log(5) + log(5x+1) = log(x+5) + log(6)
-----
log[5(5x+1)] = log[6(x+5)]
----
5(5x+1) = 6x+30
25x+5 = 6x+30
19x = 25
---
x = 25/19
==============
Cheers,
Stan H.
==============
|
|
|