Question 510130: Your club is selling candles to raise money. It costs $100 to rent a booth to sell candles. If the candles cost $1 each and are sold for $5 each, how many candle must be sold to equal your expenses?
Found 2 solutions by oberobic, solver91311:
Answer by oberobic(2304)   (Show Source):
You can put this solution on YOUR website! Profit = Total Revenue - Total Cost
.
Total Cost = Variable Cost per Unit * Number of Units Produced + Fixed Costs
.
Total Revenue = Sales Price * Units Sold
.
x = number of candles
.
TC = $1/candle * x candles + $100
.
TR = $5/candle * x
.
We want to find the point where TC =TR, which is the break-even point.
.
1x + 100 = 5x
100 = 4x
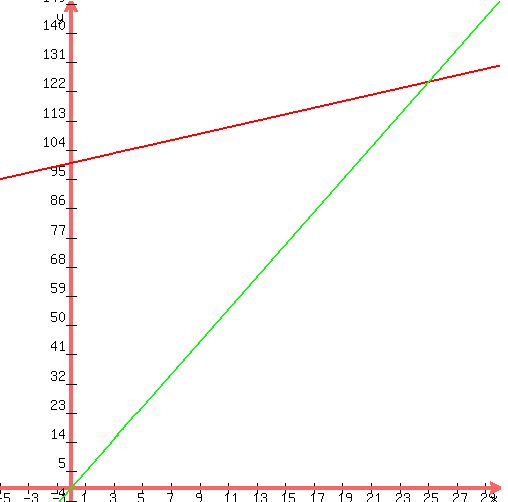
x = 25
.
So when you sell 25 candles at $5, you achieve $0 profitability.
Of course, that means you have paid your fixed costs ($100).
In turn that means the rest of your candles sales contribute profit.
.
In the following graph, the red line is TC and the green line is TR.
.
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website!
The cost as a function of the number of candles bought is 1 dollar per candle bought plus 100 dollars for the rental of the booth.
Let  represent the number of candles bought, then \ =\ x_b\ +\ 100) .
Let  represent the number sold and this number is restricted to  since you can't sell more than you buy.
The revenue received is 5 dollars per candle sold, so the revenue function is 
Profit is Revenue minus Cost, so:
\ =\ 5x_s\ -\ \left(x_b\ +\ 100\right))
Breakeven, that is when profit equals zero is when cost equals revenue:
Now if what you really wanted to know (but didn't ask, or didn't communicate effectively anyway) is what is the number to buy such that if you sell them all, you break even? For that, you set  , that is:
Now just solve for  .
Note that if you only buy that many, the BEST you can do is break even. Since the general idea of any business venture, whether for profit or for charity, is to make money, you have to buy more than this. However, this comes with risk. The more you buy, the more you have to sell in order to turn a profit. What you really need now is the services of a market research firm that can tell you, within certain statistical limits, what your demand function is. That is, at any given price point within some sort of reasonable limits, how many candles you can expect to sell.
John
My calculator said it, I believe it, that settles it
|
|
|
