SOLUTION: Can you help me write each linear in slope-intercept form then graph the inequality 2x-3y>7

In order to graph an inequality we first have to draw the graph of 
the boundary, which is the equation formed by replacing the inequality
sign > by =

First we draw the graph of 

2x - 3y = 7

We put it in slope intercept form:

Add -2x to both sides:

   -3y = -2x + 7

Divide every number by -3

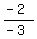 y = x +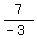 

Simplify:

     y = x - 

The y-intercept is at  on the y-axis, the slope is 

So we start at the y-intercept (0,) or (0,),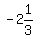
See the little dot about 1/3 of the way from -2 toward -3:



Then we notice that the numerator of the slope is 2, so we draw a line
from the y-intercept 2 units upward:



Then we notice that the denominator of the slope is 3, so from the end
of that line (where the arrowhead is) we draw another line 3 units to
the right:




Next we draw the boundary line through the y-intercept and the second arrowhead.
We draw it as a dotted line because the inequality is > and not >. The
solution does not include the boundary line.



Next we must find out whether we are to shade the region above the dotted 
boundary line, or the region below it.

So we choose any arbitrary TEST POINT that does not lie on the dotted 
boundary line, say the point (x,y) = (2,3)



and substitute it into the original
inequality:

    2x - 3y > 7
2(2) - 3(3) > 7
      4 - 9 > 7
         -5 > 7

That is false, so (2,3) is NOT a solution, so that means that the 
solutions are NOT on the upper side of the boundary line so we 
shade the lower side of the line, like this:



That bright red shaded area is the graph of the inequality.

Edwin