Question 507225: n^2+4n-12
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Looking at the expression 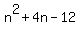 , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is  . .
Now multiply the first coefficient  by the last term by the last term  to get to get  . .
Now the question is: what two whole numbers multiply to  (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of  (the previous product). (the previous product).
Factors of  : :
1,2,3,4,6,12
-1,-2,-3,-4,-6,-12
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*(-12) = -12
2*(-6) = -12
3*(-4) = -12
(-1)*(12) = -12
(-2)*(6) = -12
(-3)*(4) = -12
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | -12 | 1+(-12)=-11 | | 2 | -6 | 2+(-6)=-4 | | 3 | -4 | 3+(-4)=-1 | | -1 | 12 | -1+12=11 | | -2 | 6 | -2+6=4 | | -3 | 4 | -3+4=1 |
From the table, we can see that the two numbers  and and  add to add to  (the middle coefficient). (the middle coefficient).
So the two numbers  and and  both multiply to both multiply to  and add to and add to 
Now replace the middle term 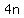 with with 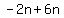 . Remember, . Remember,  and and  add to add to  . So this shows us that . So this shows us that  . .
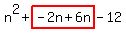 Replace the second term Replace the second term 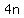 with with 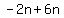 . .
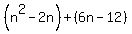 Group the terms into two pairs. Group the terms into two pairs.
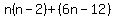 Factor out the GCF Factor out the GCF  from the first group. from the first group.
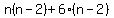 Factor out Factor out  from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis. from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis.
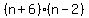 Combine like terms. Or factor out the common term Combine like terms. Or factor out the common term 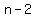
===============================================================
Answer:
So 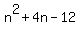 factors to factors to 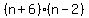 . .
In other words,  . .
Note: you can check the answer by expanding 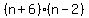 to get to get 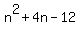 or by graphing the original expression and the answer (the two graphs should be identical). or by graphing the original expression and the answer (the two graphs should be identical).
Let me know if you need more help or if you need me to explain a step in more detail.
Feel free to email me at jim_thompson5910@hotmail.com
or you can visit my website here: http://www.freewebs.com/jimthompson5910/home.html
Thanks,
Jim
|
|
|