SOLUTION: It takes a man 23 min. longer to jog 5 mi than it takes his son to run the same distance. However, if the man doubles his rate, he can run the distance in 1 min. less than his son.

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: It takes a man 23 min. longer to jog 5 mi than it takes his son to run the same distance. However, if the man doubles his rate, he can run the distance in 1 min. less than his son.      Log On


   

Question 505896: It takes a man 23 min. longer to jog 5 mi than it takes his son to run the same distance. However, if the man doubles his rate, he can run the distance in 1 min. less than his son. What is the man's rate of jogging and what is the son's rate of running?
Found 2 solutions by stanbon, MathTherapy:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
It takes a man 23 min. longer to jog 5 mi than it takes his son to run the same distance. However, if the man doubles his rate, he can run the distance in 1 min. less than his son. What is the man's rate of jogging and what is the son's rate of running?
----
Father DATA:
distance = 5 mi ; time = t+(23/60) hrs ; rate = d/t = 5/[t+(23/60)] mph
----------------
Son DATA:
distance = 5 mi ; time = t hrs ; rate = d/t = 5/t mph
-----
New Father DATA:
distance = 5 mi; rate = 10/[t+(23/60)] mph ; time = d/r = [t+(23/60)]/2 hrs
----
Equation:
son time - new father time = 1/60 hr
t - [t+(23/60)]/2 = 1/60
2t - t - (23/60) = 1/60
t = 22/60 hr = 22 minutes (son's time)
Son's rate = 5mi/(11/60)hr = 300/11 = 27.27 mph
-----
father time = t+(23/60) = 45 minutes
Father's rate = 5mi/(3/4)hr = 20/3 = 6 2/3 mph
===================================================
Cheers,
Stan H.
==============

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

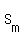Let man’s rate be S%5Bm%5D miles per hr
Then man’s time to jog 5 miles = 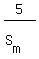5%2F%28S%5Bm%5D%29
Let son’s rate beS%5Bs%5D miles per hr
Then son’s time to jog 5 miles = 5%2F%28S%5Bs%5D%29
Since man takes 23 min longer than his son to jog 5 miles, then we have: man’s time – son’s time = 23 mins, or:

5%2F%28S%5Bm%5D%29+-+5%2F%28S%5Bs%5D%29+=+23%2F60

Since doubling the man’s rate would make him cover the 5 miles in 1 min less than son, then we can say that: son’s time - man’s time = 1 min, or:

5%2F%28S%5Bs%5D%29+-+5%2F%282S%5Bm%5D%29+=+1%2F60 ----- -%285%2F2S%5Bm%5D%29+%2B+5%2F%28S%5Bs%5D%29+=+1%2F60

We now have:
5%2F%28S%5Bm%5D%29+-+5%2F%28S%5Bs%5D%29+=+23%2F60 ---- eq (i)

-%285%2F2S%5Bm%5D%29+%2B+5%2F%28S%5Bs%5D%29+=+1%2F60 ---- eq (ii)

5%2F%28S%5Bm%5D%29+-+5%2F%282S%5Bm%5D%29+=+23%2F60+%2B+1%2F60 ------- Adding eqs (i) & (ii)

5%2F%28S%5Bm%5D%29+-+5%2F%282S%5Bm%5D%29+=+2%2F5 ----- Reducing right-side of equation

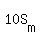
50+-+25+=+4S%5Bm%5D ------- Multiplying by LCD, 10S%5Bm%5D

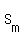4S%5Bm%5D+=+25

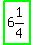S%5Bm%5D, or man's speed = 25%2F4, or highlight_green%286%261%2F4%29 mph



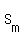5%2F%2825%2F4%29+-+5%2F%28S%5Bs%5D%29+=+23%2F60 ---- Substituting 6%261%2F4 or 25%2F4 for S%5Bm%5D in eq (i)

4%2F5+-+5%2F%28S%5Bs%5D%29+=+23%2F60

-+%285%2FS%5Bs%5D%29+=+23%2F60+-+4%2F5

-+%285%2FS%5Bs%5D%29+=+23%2F60+-+48%2F60

-+%285%2FS%5Bs%5D%29+=+-+25%2F60

-25S%5Bs%5D+=+-+300 ----- Cross-multiplying

S%5Bs%5D, or son's speed = %28-300%29%2F%28-25%29, or highlight_green%2812%29 mph

-----------
Check
-----------
Man’s time = son’s time + 23 mins
5%2F%286%261%2F4%29+=+5%2F12 + 23 mins

5%284%2F25%29+=+5%2F12+%2B+23%2F60

4%2F5+=+25%2F60+%2B+23%2F60

4%2F5+=+48%2F60

4%2F5+=+4%2F5 (TRUE)

Doubling speed, man’s time = son’s time – 1 min
5%2F%282%2A%286%261%2F4%29%29+=+5%2F12 - 1 min

5%2F%282%2A%2825%2F4%29%29+=+5%2F12+-+1%2F60

5%2F%2825%2F2%29+=+5%2F12+-+1%2F60

2%2F5+=+25%2F60+-+1%2F60

2%2F5+=+24%2F60

2%2F5+=+2%2F5 (TRUE)

Send comments and “thank-yous” to MathMadEzy@aol.com