|
Question 499523: please help me solve this equation f(x) 2x squared + 16x+28
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! equation is:
2x^2 + 16x + 28
set the equation equal to 0.
you get:
2x^2 + 16x + 28 = 0
divide both sides of the equation by 2.
you get:
x^2 + 8x + 14 = 0
factor the equation.
since this is a quadratic equation, and since the middle term is positive and the last term is positive, your factors will be a combination of:
(x + a) * (x + b)
if you can find a and b, then you can successfully factor the equation.
if you have difficulty finding a and b, then you need to resort to the quadratic formula to find them.
the quadratic formula is your formula of last resort if you can't find the factors by other, more obvious means, like factoring.
we'll try to factor first.
we need to find a and b such that a*b = 14 and a+b = 8
14 is equal to 2 * 7 but 2 and 7 add up to 9 so they're no good.
it doesn't look like we'll be able to find the factors this way.
we'll jump to the quadratic formula.
the quadratic formula is:
x = (-b +/- sqrt(b^2-4ac)/(2a)
the formula looks like this:
x = 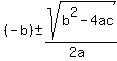
the standard form of a quadratic equation is:
ax^2 + bx + c = 0
a is the coefficient of the x^2 term.
b is the coefficient of the x term.
c is the constant term.
your equation is:
x^2 + 8x + 14 = 0
a = 1
b = 8
c = 14
replacing a, b, and c in the quadratic formula with the values of 1, 8, and 14 gets:
x = (-8 +/- sqrt(8^2-4*1*14)/(2*1)
this becomes:
x = (-8 +/- sqrt(8)/2 which becomes:
x = -4 +/- sqrt(8)/2
now sqrt(8) is equal to sqrt(2*4) which is equal to 2*sqrt(2).
our equation becomes:
x = -4 +/- 2*sqrt(2)/2 which becomes:
x = -4 +/- sqrt(2)
that's what your answer looks like it will be.
to confirm this is a good answer, we substitute it in the original equation to see if that equation holds true.
the original equation is:
2x^2 + 16x + 28
we replace x with:
-4 + sqrt(2) and then we replace x with:
-4 - sqrt(2).
the easy way to do this is to resolve the answer to a single number which is stored in the calculator and then used in place of x in the equation.
first we replace x with -4 + sqrt(2).
-4 + sqrt(2) = -2.585786438 which is stored in the calculator and used in place of x in the original equation.
when x = -2.585786438, 2x^2 + 16x + 28 becomes equal to 0
x = -4 + sqrt(2) is confirmed as good.
we now replace x with -4 - sqrt(2).
-4 - sqrt(2) = -5.414213562 which is stored in the calculator and used in place of x in the original equation.
when x = -5.414213562, 2x^2 + 16x + 28 becomes equal to 0
x = -4 - sqrt(2) is confirmed as good.
the equation has been solved.
the roots of the equation are:
x = -4 + sqrt(2)
x = -4 - sqrt(2)
a graph of this equation is shown below:

the solution to the quadratic equation is the value of x when y = 0.
in this case the solution is real so you can see it on the graph.
---------
your problem has been solved above.
the information below is additional information you may or may not find interesting.
it is useful to know because you will eventually run into situations the same as those expressed below.
-----------
in other cases, the solution will not be real so you won't be able to see it on the graph.
an example where the solution is not real is shown below:
2x^2 + 16x + 58 = 0
graph of this equation is:

this equation also has roots, but they are not real.
if we solve this equation, we will see that the value of x becomes:
x = -4 +/- 4*sqrt(-13).
that negative value under the square root sign is what makes the solution not real because there is no real number that is the square root of (-13).
these are the roots, but they are not real.
this solution is called a complex solution.
a complex solution has a real part and an imaginary part.
the real part of this solution is the -4.
the imaginary part of this solution is +/- 4*sqrt(-13).
if you know how to operate with complex numbers, then you will find that these roots do lead to a value of y = 0 when x = -4 + 4*sqrt(-13) and when x = -4 - 4*sqrt(-13). since you don't, at this time, deal with complex number, then you say that the equation has no roots because the roots you are looking for are only real numbers and not complex numbers.
on the graph, the fact that the equation doesn't cross the x-axis is your clue that this equation would not have real roots.
in the quadratic formula, the fact that the expression under the square root sign is negative is your clue that this quadratic equation doesn't have real roots.
----------------
for the problem that you did provide, there are real roots because the graph of the equation does cross the x-axis and the expression under the square root sign is positive.
those roots are, once again:
x = -4 + sqrt(2) and:
x = -4 - sqrt(2)
|
|
|
| |