A fair die is rolled 10 times. What is the probability that an odd number (1, 3 or 5) will occur between 2 and 4 times (inclusive)?
That's a binomial probability problem.
There are three ways, (1) By formula, (2) By table, (3) By TI-84 calculator
(1) By formula




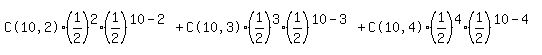

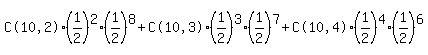



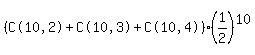
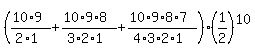

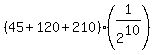

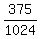
 .3662109375
(2) By table. There are two kinds of binomial tables, cumulative and
non-cumulative.
Go to the binomial table for n=10, find the row for x (or r on some tables)
as 4 and go across to the column headed .5 or .50.
A. If your table is cumulative, then you will read .3770.
1. find the row for x=2 and go across to the column headed .5 or .50, and
read .0107
2. Subtract .3770-.0107 = .3663
B. If your table is not cumulative, you will read .2051.
1. find the row for x=3 and go across to the column headed .5 or .50, and
read .1172
2. find the row for x=2 and go across to the column headed .5 or .50, and
read .0439
3. Add .2051+.1172+.0439 and get .3662.
(3) By TI-84 calculator
Press 2nd
Press VARS ALPHA APPS
If you have older version, you will see
binomcdf(10,.5,4
)
If you have the newer version you have to first answer
trials:10, p:.5, x value: 4, highlight and click Paste
Press ENTER
Press — (minus)
Press 2nd
Press VARS ALPHA APPS
If you have older version, you will see
binomcdf(10,.5,4
)-binomcdf(10,.5
,1)
If you have the newer version you first have to answer
trials:10, p:.5, x value: 1, highlight and click Paste
Press ENTER
Read .3662109375
Edwin
.3662109375
(2) By table. There are two kinds of binomial tables, cumulative and
non-cumulative.
Go to the binomial table for n=10, find the row for x (or r on some tables)
as 4 and go across to the column headed .5 or .50.
A. If your table is cumulative, then you will read .3770.
1. find the row for x=2 and go across to the column headed .5 or .50, and
read .0107
2. Subtract .3770-.0107 = .3663
B. If your table is not cumulative, you will read .2051.
1. find the row for x=3 and go across to the column headed .5 or .50, and
read .1172
2. find the row for x=2 and go across to the column headed .5 or .50, and
read .0439
3. Add .2051+.1172+.0439 and get .3662.
(3) By TI-84 calculator
Press 2nd
Press VARS ALPHA APPS
If you have older version, you will see
binomcdf(10,.5,4
)
If you have the newer version you have to first answer
trials:10, p:.5, x value: 4, highlight and click Paste
Press ENTER
Press — (minus)
Press 2nd
Press VARS ALPHA APPS
If you have older version, you will see
binomcdf(10,.5,4
)-binomcdf(10,.5
,1)
If you have the newer version you first have to answer
trials:10, p:.5, x value: 1, highlight and click Paste
Press ENTER
Read .3662109375
Edwin