|
Question 499019: Please tell me how I would graph this. The question is:
Graph the solution set of the following system of inequalities:
x^2+y^2 less than or equal to 25
y greater than or equal to |x|
Found 2 solutions by chessace, Theo:
Answer by chessace(471)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first one results in the inside (and boundary) of a circle with center at (0,0) and radius = 5.
The 2nd one eliminates everything with negative y and everything below the lines y=x (to the right or NorthEast) and y=-x (to the left or NorthWest).
So the final graph will be the border and interior of a "piece of pie", a right angle at the point (0,0), "crust" at the top.
(> rotated 90 degrees clockwise.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! to graph them, you make the inequality an equality and then you solve for y.
y >= |x| becomes y = |x|.
you can graph it as such.
x^2 + y^2 <= 25 becomes x^2 + y^2 = 25
subtract x^2 from both sides of the equation to get y^2 = 25 - x^2
take the square root of both sides of the equation to get y = +/- sqrt(25 - x^2)
you can graph it as such.
the equations you are graphing are:
y = |x|
y = +/- sqrt(25-x^2)
your graph will look like this:
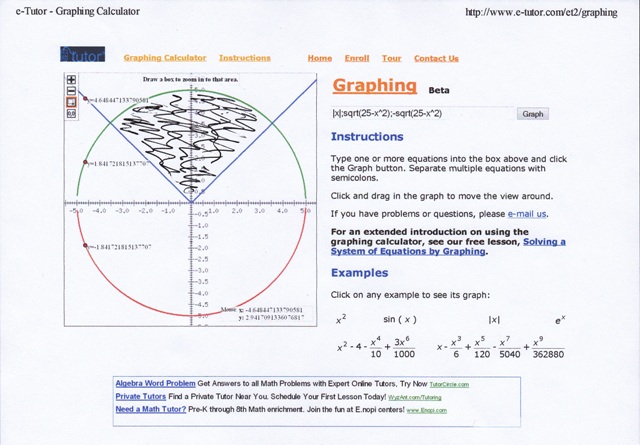
now you have to go back to the inequality and figure out which part of this graph is what you want.
we'll start with y >= |x|
if x is positive, then this is equivalent to y >= x.
if x is negative, then this is equivalent to y >= -x.
regardless of whether x is positive or negative, y will always be positive.
in both cases the value of y will be on the line of the graph or above it.
next we'll work on x^2 + y^2 <= 25
we subtract x^2 from both sides of the equation to get:
y^2 <= 25 - x^2
we take the square root of both sides of this equation to get:
y <= sqrt(25 - x^2) and y >= -sqrt(25 - x^2)
this may be a little hard to see, but it has to be this way in order for y^2 to be smaller than or equal to 25 - x^2.
in our example, we are only concerned with y <= sqrt(x) because we are restricted to positive values of y since y has to be >= |x|.
the shaded area in the graph shows you the area of the graph that is compatible with the requirements of the problem.
y >= |x| puts y above the graph of that equation.
y <= sqrt(25 - x^2) puts y within the boundaries of the circle.
|
|
|
| |