|
Question 495075: Can you give me lots of examples, and the definition of a real number, rational number, irrational number, and integers. Please and thank you.
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
REALS:
All numbers that are not imaginary are REAL numbers.
INTEGERS:
The INTEGERS consist of the counting numbers 1,2,3,4,...
and zero 0 and also the negatives of the counting numbers,
-1,-2,-3,-4,... but no numbers in between them.
RATIONALS;
The rational numbers are all the numbers you can make by
making a fraction with an integer for the numerator and an
integer for the denominator. But you cannot use 0 for a
denominator.
Here are some rational numbers  , ,  All integers are also rational numbers because, for example,
the integer 7 can be written as
All integers are also rational numbers because, for example,
the integer 7 can be written as 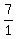 and both the numerator
and the denominator are integers.
Negative fractions such as and both the numerator
and the denominator are integers.
Negative fractions such as 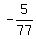 are also rational numbers
because for example are also rational numbers
because for example 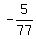 can be written as either can be written as either 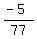 or
as or
as 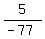 .
Decimals that end, such as 7.85 are rational because for example, 7.85
can be written as .
Decimals that end, such as 7.85 are rational because for example, 7.85
can be written as 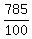 which reduces to which reduces to 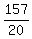 Decimals that don't end but which repeat a block of digits forever are
rational numbers, for example
Decimals that don't end but which repeat a block of digits forever are
rational numbers, for example  = 0.6666666...
3.76363636363... can be written as = 0.6666666...
3.76363636363... can be written as 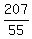 , (divide that out and see).
IRRATIONAL
These are simply numbers that are not rational. They can only
be approximated by irrational numbers or written with special symbols
such as √ ∛ ∜ or p.
When they are approximated with decimals, the decimals never repeat
a block of digits. Many people think p is the
same as the rational numbet , (divide that out and see).
IRRATIONAL
These are simply numbers that are not rational. They can only
be approximated by irrational numbers or written with special symbols
such as √ ∛ ∜ or p.
When they are approximated with decimals, the decimals never repeat
a block of digits. Many people think p is the
same as the rational numbet  . However, if you divide that out
you get . However, if you divide that out
you get
 = 3.142857142857142857...
and it keeps repeating 142857 over and over forever. However p is only close to that,
not exactly that, for the decimals of p are:
p ≈ 3.141592653589793238 and
those decimal digits go on forever with no pattern whatsoever.
(We use a wavy equal sign ≈ to indicate "approximately equal to").
When irrational numbers are approximated by decimals, they sometimes have
a pattern to the digits, such as this one:
7.2233222333222233332222233333...
but it is irrational but it doesn't repeat the same block of digits,
but increases the length of the block of 2's and 3's each time.
Edwin = 3.142857142857142857...
and it keeps repeating 142857 over and over forever. However p is only close to that,
not exactly that, for the decimals of p are:
p ≈ 3.141592653589793238 and
those decimal digits go on forever with no pattern whatsoever.
(We use a wavy equal sign ≈ to indicate "approximately equal to").
When irrational numbers are approximated by decimals, they sometimes have
a pattern to the digits, such as this one:
7.2233222333222233332222233333...
but it is irrational but it doesn't repeat the same block of digits,
but increases the length of the block of 2's and 3's each time.
Edwin
|
|
|
| |