Question 49203This question is from textbook beginning algebra
: quotient when 3 more than a number is divided by 3 less than that sam number
This question is from textbook beginning algebra
Answer by Born2TeachMath(20)   (Show Source): (Show Source):
You can put this solution on YOUR website! quotient when 3 more than a number is divided by 3 less than that sam number
This is a vocabulary question. Take it piece by piece...
"quotient" means we've got a division problem, also known as a fraction coming up. So draw yourself a horizontal fraction line.
"3 more than a number" - what does this mean? If you take any number - we need one, but they don't give us one, so let's make one up - let's use "x" as our special hidden number. So now we need 3 more than that. How do you do that? Just add three to the number. So "3 more than a number" means "3 + x".
This goes on the top of your fraction, since it says that the first part "is divided by" the second part.
OK, let's go for the second part. "3 less than that same number". First, we're using the same number, so start with x. Now we need the "3 less than that" . If you think about it, what number is 3 less than 10, for example? 7, of course, but how did you find that? You subtracted 3 FROM THE NUMBER, not the 10 from the 3. So "3 less than that number" means "x - 3". Of course, this part goes below the horizontal division line.
So the answer is 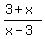
Be careful not to do "3 - x" in the bottom, since they aren't the same thing. The order that things are written with subtraction make a big difference. With addition, they don't make any difference, to the top could also be (x + 3). Think about it: 5 + 3 = 3 + 5 = 8. But 5 - 3 (not=) 3 - 5. One is positive, the other is negative.
The rest is vocabulary. If you don't know which way to write the order of numbers, just pick an actual number, and test it. See which one makes sense, and go with it.
|
|
|