SOLUTION: There is a positive two-digit integer that is divisible by the sum of its digits AND that has exactly 5 factors. What is the sum of its factors?

For any integer the numbers

A. one of its factors 

and 

B.  

are two different integers except when the integer is a
perfect square and that factor is its square root.

So only perfect squares have an odd number of factors, since
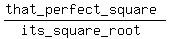its square root and  are not two different
factors, but only one factor, since those are the same number. 

So it has to be a perfect square to have 5 factors.
So it has to be one of these:

16, 25, 36, 49, 64, or 81

16 is not divisible by 1+6, which is 7

25 is not divisible by 2+5, which is 7

36 IS divisible by 3+6, which is 9.  However 36 has 
       9 factors 1,2,3,4,6,9,12,18, and 36, and that's too many.

64 is not divisible by 6+4, which is 10.

81 is divisible by 8+1, which is 9.  It's factors are 1,3,9,27, and 81.
       And that's 5, so the number is 81.

Answer: The sum of the factors is 1+3+9+27+81 = 121

Edwin