Question 489785: I need help in finding the coordinates of the vertex for the parabola defined by the given quadratic function f(x) = -x^2 -4x + 8
Found 2 solutions by lwsshak3, MathTherapy:
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! I need help in finding the coordinates of the vertex for the parabola defined by the given quadratic function f(x) = -x^2 -4x + 8
**
Given function is a parabola of the standard form: -A(x-h)^2+k, with (h,k) being the (x,y) coordinates of the vertex. A is a multiplier which affects the steepness or slope of the parabola. The minus sign of the lead coefficient means that the parabola opens downwards, that is, it has a maximum.
..
Finding the coordinates of the vertex:
f(x) = -x^2 -4x + 8
completing the square
y=-(x^2+4x+4)+8+4
y=-(x+2)^2+12
Ans:
Coordinates of the vertex: (-2,12)
See graph below as a visual check on the answer:
..

Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I need help in finding the coordinates of the vertex for the parabola defined by the given quadratic function f(x) = -x^2 -4x + 8
To find the axis of symmetry, or the x-coordinate of the vertex, we use the formula, 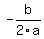 , where a = - 1, and b = - 4 , where a = - 1, and b = - 4
That results in: x = 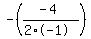 = = 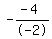 = - 2 = - 2
Now, substituting - 2 for x in the equation, we get: f(x) or y = 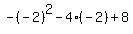 ------ f(x) or y = - 4 + 8 + 8 ----- y = 12 ------ f(x) or y = - 4 + 8 + 8 ----- y = 12
Since the x and y-coordinates are - 2, and 12, respectively, then the coordinates of the vertex of the parabola are ( , ,  ) )
Send comments and “thank-yous” to MathMadEzy@aol.com
|
|
|