|
Question 488296: Hi, I am trying to help my daughter with her Algebra and forgot how to solve for the following (y=mx+b) statement. I hope you can help as I have been out of this since my late twenties!
Write slope-intercept form of an equation of the line that passes through the given point and is parallel to the equation given.
(5,-1), y= -3/4x+1
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! The slope intercept form, as you can see, is:
.
.
m, the multiplier of the x is the slope of the line that the slope intercept equation establishes.
.
In order for a line to be parallel to a given line, it must have the same slope as the given line. The line that you were given is:
.
.
Since -3/4 is the multiplier of x, it is the slope of the graph for given line. Therefore, what you are being asked to do is to find the slope intercept line that has a slope of 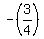 and passes through the point (5, -1). So let's begin with the general slope intercept form:
.
.
Just for your info, a slope of 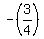can be interpreted as follows: The minus sign tells you that as the line moves to the right the graphed line drops downward. Had the sign been + the graphed line would go upward as you moved to the right. The fraction can be determined as follows. The denominator (4) tells you that for every 4 units the graph moves to the right, the drop or rise is the numerator (in this problem it is a drop of 3 units). If the multiplier of x is a whole number, for example 5, think of it as a numerator of 5 and a denominator of 1 (that is  so that for every 1 unit moved horizontally to the right, the change upward is 5 (if +) or downward 5 (if minus)).
.
We've already determined that the graph of the line that we need has a slope of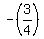
.
So substitute this into the slope intercept form and you have:
.
.
What else do you know? You know that the given point (5, -1) must satisfy this equation if it is to be on the line. So we can substitute x = 5 and y = -1 into the equation to get:
.
.
Now all you have to do is a little math and equation solving to find what b (the point where the graph crosses the y-axis) needs to be. Multiply out the first term on the right side and you have:
.
.
Add  to both sides and this reduces the equation to:
.
.
Convert -1 to -4/4 so that you can combine the two left hand terms:
.
.
.
which simplifies to:
.
.
Since you now have both m and b, you can write the equation of this new line as:
.
.
.
and the graph of these two parallel lines looks like:
.
.
The red line is the graph that you were given. (Note the negative slope (down and to the right) and that graph crosses the y-axis at y = +1 and indicated by the +1 value for b in the original equation.) The green line is the graph that we developed as given by the slope intercept form:
.
.
Note here that the slope (multiplier of x) is again 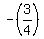, but this time the value of b (the intercept on the y-axis) is  .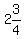
.
A great big thanks for taking the time to work with your daughter. More parents should be like you !!!
.
Hope this helps you in some small way.
|
|
|
| |
