|
Question 488099: How do you graph the following?
y=-3/4x-1
x=-2 y=1.5
x=1 y=-1.75
x=2 y=-2.5
x=-3 y=1.25
The graph points don't see to line up.
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! There are three different forms of graphs in this problem.
.
The first form is represented by the equation  . This is called the slope intercept form and the standard general form of this equation is written as  . In this general form, m which is the multiplier of the x is the slope of the graphed line. If m is positive, the graphed line goes upward as you move toward the right on the graph. But if m is negative, the graphed line goes downward as you move toward the right on the graph. Regardless of the sign, the amount of the slope is determined by saying "as I move horizontally to the right the number of units in the denominator of m, the graph goes up or down (depending on the sign) the number of units in the numerator of m. (If m is a whole number, the denominator is 1 and the numerator is the whole number.) The second thing to notice is the term 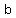 . The value of + b is the point on the y-axis where the graph crosses the axis.
.
In the first problem, m (which is the multiplier of x) is  . The minus sign tells us that the graph slants downward as you move toward the right. It also tells us that as you move horizontally 4 units from any point on the graph, at the place you reach the end of the 4 units you go down 3 units and at that location you have another point on the graph. Where is a point on this graph. Look at + (-1). The -1 is the b that is added to the x term in the equation you were given. b is the point on the graph where the graph crosses the y-axis. Therefore, this graph crosses the y-axis at -1 on the axis. From this point move 4 units (slope denominator) horizontally and then down 3 units vertically (slope numerator) and mark that location. This location is a second point on the graph. From that second point move horizontally 4 units and then vertically down 3 units and you have the third point on the graph. When you finish you should have a graph that looks like this:
.
.
Notice that from the y-axis intercept at -1, if you move 4 units horizontally to the right you will be at the point (+4, -1). Then if you move vertically down 3 units you will be at the point (4, -4) and that is a second point on the graph. Then you can move 4 more units horizontally to the right from this second point and you will be at (8, -4). Then go vertically down 3 units and you will be at the point (8, -7) and that is a third point on the graph.
.
That pretty much is the first problem. All the other problems involve X = a constant and y = another constant.
.
x = a constant means that no matter what value y may take, x will always be the same. The graph of this will be a vertical line that crosses the x-axis at the constant. Similarly, for y = a constant, that means that no matter what value x is, the corresponding value of y is the constant. The graph of this will be a horizontal line that crosses the y-axis at the constant.
.
Second problem: x = -2 and y = 1.5. The two graphs are as shown:
.
.
Notice that the vertical red line is the graph of x = -2 and the horizontal green line is the graph of y = +1.5. The common solution for these two graphs is the point where the red graph and the green graph cross at the point (-2, 1.5).
.
Third problem: x=1 y=-1.75. The two graphs are as shown:
.
.
Notice that the red graph is the graph of x = +1 and the green graph is the graph of y = -1.75.
.
The pair of graphs has as a common solution the point (1, -1.75)
.
Fourth problem: x=2 y=-2.5. The two graphs are:
.
.
Make sure that you understand why these graphs look as they do and what the common solution for these two graphs is.
.
Finally, the Fifth problem: x=-3 y=1.25
.
.
Study this graph also so that you thoroughly understand how to graph x = constant and y = constant.
.
Hope this helps you with understanding these problems.
|
|
|
| |
