Question 487753: Respected Sir ,
Please help me to solve this question, I will be very grateful for your help
If there are two groups with 75 and 65 as harmonic means and containing 15 and 13 observations then the combined HM is given by
As the answer given is : 70.36
Please help me to simplify this !!!
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think it would be a weighted average that we are looking for.
the group with an average of 75 harmonic means had 15 observations.
the group with an average of 65 harmonic means had 13 observations.
the answer given is 70.36
the quick way is to test my hypothesis and see if it comes up with the right answer.
(75 * 15 + 65 * 13) / (15 + 13) = (1125 + 845) / (28) = (1970) / (28) = 70.35714286 which rounds off to 70.36
my hypothesis was correct.
you are taking a weighted average.
that's your answer.
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If there are two groups with 75 and 65 as harmonic means and containing 15 and 13 observations
then the combined HM is given by
As the answer given is : 70.36
~~~~~~~~~~~~~~~~~~~~~~~~
The answer 70.36, to which you refer, is INCORRECT.
The solution by @Theo is INCORRECT, too.
See my solution below.
According to the problem, we have a set of 15 numbers  , ,  , . . . , , . . . , 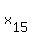 and the set of 13 numbers
and the set of 13 numbers  , ,  , . . . , , . . . , 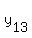 such that such that
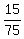 = = 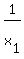 + + 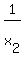 + . . . + + . . . + 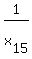 , (1) , (1)
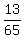 = =  + +  + . . . + + . . . + 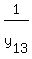 . (2)
We want to find the harmonic mean H of the union set < . (2)
We want to find the harmonic mean H of the union set <  > U < > U < 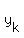 >.
It is >.
It is
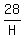 = = 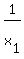 + + 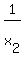 + . . . + + . . . + 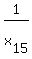 + +  + +  + . . . + + . . . + 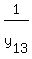 . (3)
We represent this long sum as the sum of two addends in parentheses . (3)
We represent this long sum as the sum of two addends in parentheses
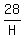 = ( = ( 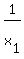 + + 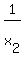 + . . . + + . . . + 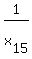 ) + ( ) + (  + +  + . . . + + . . . + 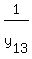 ).
Next, we replace each of the two sums in parentheses by their values from (1) and (2) ).
Next, we replace each of the two sums in parentheses by their values from (1) and (2)
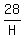 = = 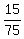 + + 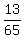 ,
and calculate ,
and calculate
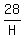 = = 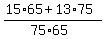 = = 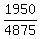 = =  Now find
H =
Now find
H =  = =  = 14*5 = 70.
ANSWER. The combined harmonic mean is 70. = 14*5 = 70.
ANSWER. The combined harmonic mean is 70.
At this point, the problem is solved completely.
The answer 70.36, to which you refer, is INCORRECT.
The solution by @Theo is INCORRECT, too.
|
|
|