Question 4873: I am completely stuck on this problem. Help!
Graph the fuction:
Answer by longjonsilver(2297)   (Show Source):
You can put this solution on YOUR website! graphing....learn the basic shapes first then apply that knowledge to more complicated ones. So  (or any exponential function) looks like:
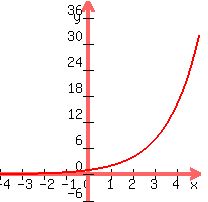
Note 2 things:
1. it does not go below the x-axis, since there is no value of x that can make y negative. In fact as x becomes more negative, the curve approaches the x-axis, ie approaches y=0. This "approaching, but never quite reaching" characteristic is called the asymptote.
2. the curve rises rapidly to infinity as x increases.
So, what about  ? First thing is USE BRACKETS!!!! because i do not know if you mean  or  . So i shall do both!
1.
we know the rough shape. Just need to know the asymptote and any values where the curve crosses the axes.
Any value of x gives a whole range of possible values of 4x+4. All of these, as powers of 2 will never give a negative answer for y. So the curve, again, does not go below the x-axis...ie the asymptote is y=0.
Voila, all we need now is find where the curve crosses the y=axis (ie where x=0)...  -->  -->  --> y=16.
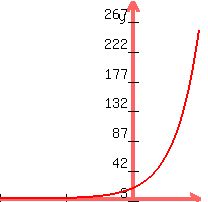
see how this is exactly the same type of curve but the axes scales are hugely different.
2.
Again, we know the rough shape..any value of x will never give a negative answer, so never below y=0. However, we then add 4 to all answers, so our asymptote is now no longer y=0, but y=4.
Find where the curve crosses the y-axis (where x=0)... -->  -->  --> y=5
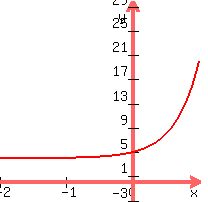
Hope this all helps. Learn the following basic shapes:
More complex versions of each type have their own characters but at least it is a start :-)
jon
|
|
|
