SOLUTION: Consider a die with eight sides marked one,two,three, and so. Assuming equally likely outcome,find the probability that the sum of two dice is the given number. Enter the answer ei

Algebra ->  Finance -> SOLUTION: Consider a die with eight sides marked one,two,three, and so. Assuming equally likely outcome,find the probability that the sum of two dice is the given number. Enter the answer ei      Log On


   

Question 487189: Consider a die with eight sides marked one,two,three, and so. Assuming equally likely outcome,find the probability that the sum of two dice is the given number. Enter the answer either as a fraction or as a decimal,round to three places
a:P(4)=
b:P(6)=
c:(10)=
d:P(11)=
e:P(14)=
f:P(16)=
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

You must make a chart for the sample space of all possible
dice throws:
 
Here is the sample space. It contains 64 possible outcomes:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

You'll find that all throws with a given sum are on a diagonal.

-----------------------------------
a:P(4)
The throws with sum 4 are in red:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

Therefore P(4) is 3 out of 64 or 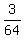3%2F64

-------------------------------------------------
b:P(6)
The throws with sum 6 are in red:


(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

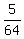Therefore P(6) is 5 out of 64 or 5%2F64

-------------------------------------------------

The throws with sum 10 are in red:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

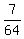Therefore P(10) is 7 out of 64 or 7%2F64

-------------------------------------------------

The throws with sum 11 are in red:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

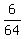Therefore P(11) is 6 out of 64 or 6%2F64 which reduces to 3%2F32

-------------------------------------------------

The throws with sum 14 are in red:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

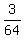Therefore P(14) is 3 out of 64 or 3%2F64

-------------------------------------------------

The throw with sum 16 is in red:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)  (1,7)  (1,8)

(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)  (2,7)  (2,8)

(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)  (3,7)  (3,8)

(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)  (4,7)  (4,8)

(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)  (5,7)  (5,8)

(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)  (6,7)  (6,8)

(7,1)  (7,2)   (7,3)  (7,4)   (7,5)  (7,6)  (7,7)  (7,8)

(8,1)  (8,2)   (8,3)  (8,4)   (8,5)  (8,6)  (8,7)  (8,8)

Therefore P(16) is 1 out of 64 or 1%2F64

-------------------------------------------------
Edwin