Question 486535: there are 5 different types of flowers. How many vases can be filled by using combinations of just 3 flowers without duplicating the 3 flowers previously used?
I'm just an old grandfather trying to help a grandson (5th grade) that I'm babysitting for. Thanks.
Found 2 solutions by deborabr, MathTherapy:
Answer by deborabr(181)   (Show Source): (Show Source):
You can put this solution on YOUR website! well, if we have 5 types of flowers we get: flower type 1, 2, 3, 4 and 5
we fill one vase with 3 types of flowers, for example: types 1,2 and 3
to fill the second vase we can take just the types of flowers 4 and 5 to don't duplicate any type of flower. so isn't possible to fill many vases with 3 types of flowers without repeat them. the response would 1 vase. i hope it helped you.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! there are 5 different types of flowers. How many vases can be filled by using combinations of just 3 flowers without duplicating the 3 flowers previously used?
To do this, we need to use a combination of 3 flowers from 5 flowers, or 5C3, which calculates to: 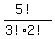 ----- ----- 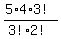 ------ ------ 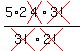 ----- ----- 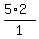 = 10 vases. = 10 vases.
Hypothetically, suppose these 5 different flowers also had different colors. We could name them as follows: R (red), W (white), P (pink), Y (yellow), and B (blue)
These are the different arrangements:
Vase 1: RWP
Vase 2: RWY
Vase 3: RWB
Vase 4: RPY
Vase 5: RPB
Vase 6: RYB
Vase 7: WPY
Vase 8: WPB
Vase 9: WYB
Vase 10: PYB
As seen, each vase will have a different 3-color combination. As such, there are  different combinations. different combinations.
|
|
|