|
Question 486125: Translate the following situation into an inequality. Do not solve
"Janice and Leonard together would like to save more than $3,500. They have saved $425 saved so far. Janice can save $120 more than twice what Leonard can save each month. How much money will they each need to save to reach their goal?"
Found 2 solutions by chessace, MathTherapy:
Answer by chessace(471)   (Show Source): (Show Source):
You can put this solution on YOUR website! J = how much money Janice needs to save.
L = similar.
J + L = 3500 - 425
J > 120 + 2L (this is the algebraic translation from English)
J - 2L > 120 or even J -2L -120 > 0 are other ways of expressing this inequality.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Translate the following situation into an inequality. Do not solve
"Janice and Leonard together would like to save more than $3,500. They have saved $425 saved so far. Janice can save $120 more than twice what Leonard can save each month. How much money will they each need to save to reach their goal?"
Since they’ve already saved $425, they still need to save another $3,075 ($3,500 – 425)
Let amount that Leonard needs to save to reach goal be L
Then amount that Janice needs to save to reach goal = L + 2L + 120
With both saving to reach goal, we have: L + 2L + 120 > 3,075
Since Leonard’s amount to reach goal is L, then solving for L, we get:
3L + 120 = 3,075 ------- 3L = 2,955 -------- L = 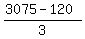 . Leonard's . Leonard's 
Since Leonard's  , then Janice's , then Janice's 
Send comments and “thank-yous” to MathMadEzy@aol.com
|
|
|
| |