Question 484041: Use the Pythagorean Theorem to find the distance between X(7,11) and Y(-1,5)
Found 2 solutions by cleomenius, MathTherapy:
Answer by cleomenius(959)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, plot your points on a graph.
Plot a point that will connect the two and form a right triangle, I formed the point Z( 7,5)
Now, determine the disance between points
7 + 1 = 8 YZ
11- 6 = 5 XZ
Use the formula a^2 + b^2 = c^2 to find the distance from XY.
8^2 + 5^2 = 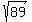 This is our answer. This is our answer.
Cleomenius.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the Pythagorean Theorem to find the distance between X(7,11) and Y(-1,5)
Let the third coordinate point of the right triangle be W.
If diagram is drawn, it’ll be seen that in order to get W (the third x-coordinate point of the right triangle), we simply subtract the smaller of the two x-coordinates from the larger. In this case, 7 – (- 1), or 7 + 1 = 8. We do the same for the y-coordinate, as follows: 11 – 5 = 6.
This means that YW (horizontal line that’s parallel to the x-axis) has a length of 8, and XW (the vertical line that’s parallel to the y-axis) has a length of 6.
With this, we can now find YX using the Pythagorean theorem. Therefore, we can say that:





10 = XY
Therefore, distance = XY =  units units
---------
Check
---------
The distance formula,  , can be used to verify the correctness of this answer. , can be used to verify the correctness of this answer.
Send comments and “thank-yous” to MathMadEzy@aol.com
|
|
|