How do you find the side lengths of an isosceles triangle if you just have the other 2 side lengths and not the perimeter?
Since the triangle is isosceles, the third side has to have one of the
two given lengths.
Sometimes there are
1. Infinitely many solutions.
Sometimes there are
2. two solutions.
Sometimes there is
3. just one solution.
Case 1 is when the two given sides are equal in length.
Then the two given sides are the legs, and the base can have any
positive length less than twice the length of one of the given
sides. That gives an infinite number of solutions.
For the other two cases. let S be the shorter length and
L be the longer.
There is always a solution in which the two legs have the longer
length L, and the base has the shorter length S.
There is sometimes a second solution where the two legs have
length S. If the triangular inequality holds with the legs having
length S, then
S+S > L
2S > L
S >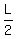 
then there is a second solution.
So we can say:
1. If the two given lengths are equal, there are infinitely many solutions.
2. If the shorter given length is greater than half the longer given
length, there are 2 solutions.
3. If the shorter given length is equal to or less than one-half the longer
given length, there is only 1 solutions.
Edwin
.
