Question 482737: Hi, I'm trying to do my precalc honors summer work, and I'm completely stuck on how to solve G(x)=x^3-8; I know it seems simple, but its although as soon as I get out of school for the summer, I completely forget how to do anything slightly complicated. Could you please explain to me how to create a table with enough points so that I can graph it by hand? Also, is there a vertex formula? It seems like there would be a vertex with this type of graph. I think the shape of it should be similar to that of an "S" because it is x^3, am I correct? Thank you, Jess
Found 2 solutions by stanbon, tinbar:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, I'm trying to do my precalc honors summer work, and I'm completely stuck on how to solve G(x)=x^3-8; I know it seems simple, but its although as soon as I get out of school for the summer, I completely forget how to do anything slightly complicated. Could you please explain to me how to create a table with enough points so that I can graph it by hand? Also, is there a vertex formula? It seems like there would be a vertex with this type of graph. I think the shape of it should be similar to that of an "S" because it is x^3, am I correct?
-------------
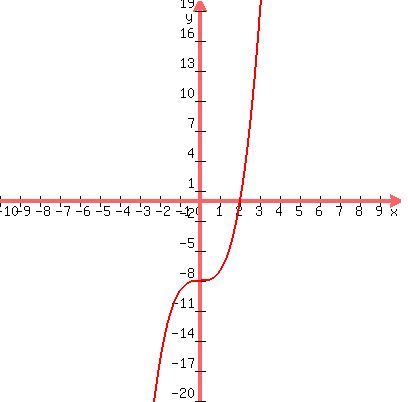
G(x) = x^3-8
---
Form is "difference of cubes"
G(x) = (x-2)(x^2+4x+4)
----
Graph: Looks like x^3 but it is lower by 8
---------------------
====================
Cheers,
Stan H.
========
Answer by tinbar(133)   (Show Source): (Show Source):
You can put this solution on YOUR website! It's actually an S sideways, and there's no vertex, how can there by on an S shape?
If your using calculus to do this, you can get special points. 1) solve G(x) = 0, i believe x = 2 is the only solution (in real numbers anyway). Then differentiate G(x), and solve G'x = 0. Only solution should be x =0. Then using the derivative find out where the function increases and where it decreases. That should be ample info for a rough graph
|
|
|