|
Question 482448: c is the midpoint of ab, d is the midpoint of ac, e is the midpoint of ad, f is the midpoint of ed, g is the midpoint of ef, and h is the midpoint of db. if dc is =16 find gh.
Found 2 solutions by cleomenius, MathTherapy:
Answer by cleomenius(959)   (Show Source): (Show Source):
You can put this solution on YOUR website! I set up a column, resembling as follows with a = 0 and b=1
Then I assigned values to the midpoints.
a| 0
b| 1
c| 0.5
d| 0.25
e| 0.125
f| 0.1875
g| 0.156
h| 0.625
Then, I set up a proportion 16/.25 = x/.469
The result I obtained was 30.016.
Cleomenius.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! c is the midpoint of ab, d is the midpoint of ac, e is the midpoint of ad, f is the midpoint of ed, g is the midpoint of ef, and h is the midpoint of db. if dc is =16 find gh.
It’s given that DC = 16, but since we know that DC = ¼AB (½ of ½AB), we can say that: ¼AB = 16. This means that AB = 64.
GF = 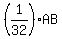 , or , or 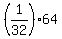 , or 2, and FD = , or 2, and FD = 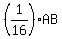 , or 4. Also, we can see that AD = ¼(AB), or ¼(64), or 16. , or 4. Also, we can see that AD = ¼(AB), or ¼(64), or 16.
Now, since AB = 64, and AD = 16, then DB must = 48 (64 – 16). And, since it was given that H is the midpoint of DB, it follows that DH = HB = ½DB, or ½(48), or 24.
Since GH = GF + FD + DH, then GH = 2 + 4 + 24 =  . .
|
|
|
| |