SOLUTION: Pls Help me with this question urgently,thanks. Find the three numbers in a geometric progression whose sum is 28 and whose product is 512.

Let a = the first number
Let r = the common ratio of the geometric progression

Then ar = 2nd number
and  ar² = 3rd number

>>...sum is 28...<<

a + ar + ar² = 28

a(1 + r + r²) = 28

>>...product is 512...<<

(a)(ar)(ar²) = 512

        a³r³ = 512

Take cube roots of both sides
                ___
          ar = ∛512

          ar = 8

           a =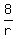  

Substitute in             

a(1 + r + r²) = 28

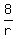(1 + r + r²) = 28

Multiply both sides by r

        8(1 + r + r²) = 28r

Divide both sides by 4

        2(1 + r + r²) = 7r

         2 + 2r + 2r² = 7r

         2r² - 5r + 2 = 0

Factor the left side:

      (2r - 1)(r - 2) = 0

  2r - 1 = 0       r - 2 = 0  
     
      2r = 1           r = 2

       r = 


So we have two solutions for r

Using r = 

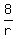           a =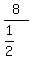  

           a = 

           a =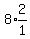  
 
           a = 16

So one solution is these three numbers using a = 16 and r = :

a, ar, ar² or 16, 8, 4

Using r = 2

           a =  

           a = 

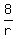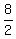           a = 4

So one solution is these three numbers using a = 4 and r = 2:

a, ar, ar² or 4, 8, 16


Solutions: 16,8,4  or 4,8,16


Edwin