Question 481549: a survey of flower gardeners showed the following:
87 grew roses,
27 grew tulips,
26 grew orchids,
15 grew both roses, and tulips,
11 grew both orchids and tulips,
19 grew both roses and orchids,
8 grew all three types,
7 grew none of these three.
create a venn diagram to reflect the data above, label diagram clearly.
use diagram to answer the questions
a) how many grew only orchids?
b) how many grew both roses and orchids, but no tulips?
c)how many grew only roses.
d) how many grew none of these three, or only tulips?
e) how many flower gardeners were surveyed?
Answer by Theo(13342)   (Show Source): (Show Source):
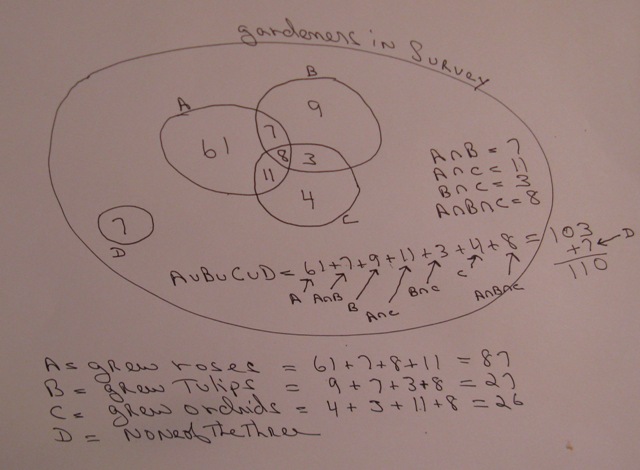
You can put this solution on YOUR website! the number of gardeners in total is equal to 103.
61 grew roses only.
9 grew tulips only.
4 grew orchids only.
----
7 grew roses and tulips only
3 grew tulips and orchids only
11 grew roses and orchids only
-----
8 grew roses and tulips and orchids
-----
7 grew none of the three (roses, tulips, or orchids)
-----
if you add roses only, and roses and tulips only, and roses and orchids only, and roses and tulips and orchids, then you get a total of 61 + 7 + 11 + 8 = 87
-----
if you add tulips only, and roses and tulips only, and tulips and orchids only, and roses and tulips and orchids, then you get 9 + 7 + 3 + 8 = 27
-----
if you add orchids only, and tulips and orchards only, and roses and orchids only, and roses and tulips and orchids, then you get 4 + 3 + 11 + 8 = 26
-----
these number agree with the numbers initially given, so you can assume that the recalculations was done correctly.
the total number of gardeners is 110.
that would be 103 plus 7 for the number of gardeners who didn't plant any of the 3 above (roses, tulips, orchids).
the answer to the rest of the questions are shown below:
a)
how many grew only orchids?
4 grew only orchids.
b)
how many grew both roses and orchids, but no tulips?
11 grew both roses and orchids, but no tulips.
c)
how many grew only roses.
61 grew only roses.
d)
how many grew none of these three, or only tulips?
7 grew none of these three and 9 grew only tulips.
this would be a total of 16 that grew none of the three or only tulips.
e)
how many flower gardeners were surveyed?
a total of 110.
-----
set theory states that the union of 2 sets is equal to:
(A union B) = A + B - (A intersect B)
set theory also states that the union of 3 sets is equal to:
(A union B union C) = A + B + C - (A intersect B) - (A intersect C) - (B intersect C) + (A intersect B intersect C).
-----
if we take your original problem and assign letters to each situation, then we get:
A = 87 grew roses,
B = 27 grew tulips,
C = 26 grew orchids,
D = 7 grew none of these.
(A intersect B) = 15 grew both roses, and tulips,
(B intersect C) = 11 grew both orchids and tulips,
(A intersect C) = 19 grew both roses and orchids,
(A intersect B intersect C) = 8 grew all three types,
-----
If we apply the formula, then we get:
(A union B union C) = A + B + C - (A intersect B) - (A intersect C) - (B intersect C) + (A intersect B intersect C) becomes:
(A union B union C) = 87 + 27 + 26 - 15 - 19 - 11 + 8 = 103.
add the 7 that didn't grow any of the other 3 and you get 103 + 7 = 110 total gardeners.
the numbers agree, so we probably did this right.
----
the assumption of the problem is that the number of gardeners that did two of the three, plus the under of gardeners that did all three, were included in the numbers given for each.
under this assumption, the procedure used was as follows:
8 gardeners grew all three.
these 8 were subtracted from the number of gardeners that did two out of three.
the gardeners that did roses and tulips became 15 - 8 = 7.
the gardeners that did tulips and orchids became 11 - 8 = 3.
the gardeners that did roses and orchids 19 - 8 = 11.
once we eliminated the gardeners that did all three from the gardeners that did two out of three, we then went and subtracted the gardeners that did two out of 3 and the gardeners that did three out of three from the gardeners that did each type of flower.
the gardeners that did roses only became 87 - 7 - 11 - 8 = 61.
the gardeners that did tulips only became 27 - 7 - 3 - 8 = 9.
the gardeners that did orchids only became 26 - 3 - 11 - 8 = 4.
we now had clean sets to work with.
each set only included elements that belonged in that set.
orchids did not include orchids and tulips which did not include orchids and tulips and roses.
each set was specific to what was included in that set.
the venn diagram for this problem is shown below:
|
|
|