|
Question 480456: The following equations have infinitely many solutions
x + 3y =3
-x + 7y + 5z =18
-2x + 6y + 6z =24
Give the right hand side of the vector form of the general solution, using a parameter such as s or t. (Any lowercase letter will do as a parameter, so long as it is not x, y or z.)
FOR EXAMPLE, for the equations
x = y + 1, y = z + 1, z = x − 2
one correct answer is
[x, y, z] = [0, −1, −2] + t [1, 1, 1]
and you would enter the right hand side of this equation in the space provided:
[0, −1, −2] + t * [1, 1, 1]
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website! 
Put in +0z in the first equation and write -x as -1x
Write as an augmented matrix by erasing the letters and
replacing the equal signs by "|", and put the whole thing
in parentheses (some people use brackets):
Now we get it in echelon form:
Get a 0 where the -1 is by adding the top row to the
middle row:
Get a 0 where the -2 is by multiplying the top row by 2 and
adding it to the bottom row: 
And since that can be divided through by 6, we do so and get 
and replace the bottom row by that:
Get a 1 where the 10 is by dividing the 2nd row through by 10
---
Get a 0 where the 2 is by multiplying the middle row by -2 and
adding it to the bottom row: 
And since that can be divided through by .8, we do so and get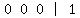 
and replace the bottom row by that:
Now it is in echelon form. Write it as a system again:
or
Oh! Oh! Look at that bottom equation:
0z = 1
There is no value of z that would make that true since
zero times any number gives 0, and cannot give 1, so there
are no solutions. So what is stated at the top, that it
has infinitely many solutions, is incorrect. It may have
been copied wrong, or there was a typo, but as it is
given above, there are no solutions to this system.
Edwin
|
|
|
| |
