SOLUTION: Please help! I am trying to learn to write the partial fraction decomposition of rational expressions such as the following: (4x^2) / (x^3+5x^2+7x+3) My book is saying someth

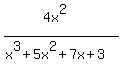
First we factor the denominator:

x³ + 5x² + 7x + 3

if we can find a zero of that polynomial then (x - that zero) is
a factor.

Since the the leading coefficient (the coefficient of x³) is 1,
all possible rational zeros are ± factor of the constant term 3
So they are ±1, ±3

We try 1 using synthetic division

1 | 1  5  7  3
  |    1  6 13
    1  6 13 16

So 1 is not a zero.

We try -1 using synthetic division

-1 | 1  5  7  3
   |   -1 -4 -3
     1  4  3  0

Yes, that left a zero remainder, So (x + 1)
is a factor and so is (x² + 4x + 3) from the
bottom line of the synthetic division. So now
we have factored 

x³ + 5x² + 7x + 3

as

(x + 1)(x² + 4x + 3)

And we can further factor the quadratic in the
second parentheses:

(x + 1)(x + 1)(x + 3)

or

(x + 1)²(x + 3)

Now the original problem:



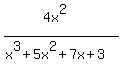becomes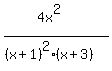 

 =  +  + 

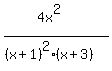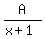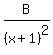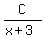(Notice that when you have a factor to a power larger than 1,
you must have a fraction with that power and all lower powers.)

Multiply through by the LCD = (x + 1)²(x + 3)

4x² = A(x+1)(x+3) + B(x+3) + C(x+1)² 

Multiplying all that out gives:

4x² = Ax² + 4Ax + 3A + Bx + 3B + Cx² + 2Cx + C

Equating the x² terms on each side:

4x² = Ax² + Cx²
  4 = A + C

Equating the x terms on each side (there are none on the left so we put 0):

0 = 4Ax + Bx + 2Cx 
0 = 4A + B + 2C

Equating the constant terms on each side: (none on the left so we put 0)

0 = 3A + 3B + C

So we have this system of equations:



Solve that system of equations and get A=-5, B = 2, C = 9

So the partial fraction decomposition is:

 =  +  + 

--------------------------------------------------  

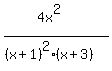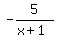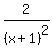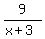There is an easier way to find A, B and C.
It's the substitution method.  When you get here:

4x² = A(x+1)(x+3) + B(x+3) + C(x+1)²

Don't multiply it out.

Substitute x = -1 to make the 1st and 3rd terms on the right 0

4(-1)² = A(-1+1)(-1+3) + B(-1+3) + C(-1+1)²
     4 = 0 + 2B + 0
     4 = 2B
     2 = B

Substitute x = -3 to make the 1st and 2nd terms on the right 0

4(-3)² = A(-3+1)(-3+3) + B(-3+3) + C(-3+1)²
    36 = 0 + 0 + 4C
    36 = 4C
     9 = C

Substitute another easy value, say x = 0, and B=2 and C=9

4(0)² = A(0+1)(0+3) + 2(0+3) + 9(0+1)²

    0 = 3A + 6 + 9
    0 = 3A + 15
  -15 = 3A
   -5 = A

 =  +  + 

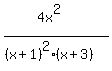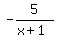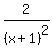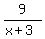With this method you don't have to multiply the whole 
thing out or solve a system of equattions.  This way is
much easier than equating like terms and solving a 
system of equations. But some teachers won't let you use 
this method, even though it always works.  Some won't 
allow it because the original problem is undefined for 
the values you have to substitute to make those 
expressions = 0, for it makes denominators = 0 in the
original problem.

Edwin