SOLUTION: <pre> ___ Given f(x) = 3<font face = "symbol">Ö</font>x-1, find f^-1 if the inverse exists. </pre>

               ___
Given f(x) = 3Öx-1 , if the inverse exist.



To do inverses you can't just learn the algebra part and skip the
graph part because you have to understand what the inverse graph
looks like because you have to know how to put in the proper
restrictions.  So be sure you understand the fact that the inverse
of a one-to-one function is its reflection across (or into) the
identity line y=x which is a 45° line through the origin.  A graph
and its inverse will always make a symmetrical figure about the
identity line y=x.
                              ___ 
Here is the graph of f(x) = 3Öx-1 


 

That curve passes the horizontal line test, so that when we
reflect it in the line y=x (blue dotted line), the green inverse
graph below passes the vertical line test and therefore is a function:



Now we need to find the equation of the green functional curve,
which is the graph of the inverse of the f(x), which is denoted
f-1(x). 

To do this, we start with the original equation:
           _____
  f(x) = 3Öx – 1

Then we change f(x) to y

           _____
     y = 3Öx – 1


Next we interchange x and y

           _____
     x = 3Öy – 1


We solve for y

Square both sides:    

            _____
  (x)² = (3Öy – 1)²

    x² = 9(y - 1)

    x² = 9y - 9

Swap sides:

9y - 9 = x²

    9y = x² + 9

Divide through by 9

     y =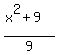 
 
and now we replace y by f-1
        
f-1(x) =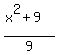 

By making two fractions and simplifying, 
that can be written equivalently as

f-1(x) = 

Either is correct if when we graph it we get the green curve above.
But we must graph it to check to see if it is the inverse or not.

That should be the equation of the green curve above which is the 
inverse of f(x)

However when we graph it, we get this: 



So we must cut off the left part of the green graph.

The way we do that is to restrict the graph to the right
side only, by requiring that x be greater than or equal 0,

So the answer is

f-1(x) = 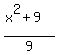, x≧0

or

f-1(x) = 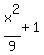,  x≧0

That way you get only the right side of that green graph:



But you MUST have the restriction x≧0 out beside it because the
whole green parabola is NOT the inverse but only the right half of it.
And the only way you would know to make that restriction is to draw
and understand the graphs.

Edwin