SOLUTION: <pre> Given f(x) = 9 – x² , x&#8807;0 , find f^-1 if the inverse exists. ___ Given f(x) = 3<font face = "symbol">Ö</font>x-1, find f^-1 if the

I'll just do the first one.

Here is the graph of f(x) = 9 – x² without the restriction x≧3

 

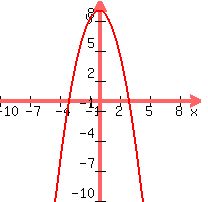As you see it does not pass the horizontal line test so its inverse,
(in green) which is its reflection in the 45° line through the origin whose
equation is y=x (the blue dotted line below) would not pass the vertical 
line test, and would not be a function, as you can see:



However with the restriction x≧0, the graph is only the
right half of the whole curve (without the restriction x≧0):

 

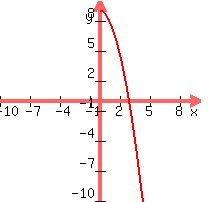Then the curve passes the horizontal line test, so that when we
reflect it in the line y=x (blue dotted line), the green inverse
graph passes the vertical line test and therefore is a function:



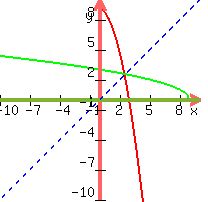Now we need to find the equation of the green functional curve,
which is the graph of the inverse of the f(x), which is denoted
f-1(x). 

To do this, we start with the original equation:

  f(x) = 9 – x²

Then we change f(x) to y

     y = 9 - x²

Next we interchange x and y

     x = 9 - y²

We solve for y

    y² = 9 - x

Using the principle of square roots:
           _____
     y = ±Ö9 - x

But we use only the + square root since the green graph of
the inverse is above the x-axis, so we have

          _____
     y = Ö9 - x
 
and now we replace y by f-1
         _____
f-1(x) = Ö9 - x

That's the equation of the green curve above which is the 
inverse of f(x)




Edwin