Question 479249: I need to know what the linear equation would be for the following word problem:
A teacher is given a $300 stipend for supplies. Company A offers a 15% discount, but Company B offers a 20% discount after the first $20 spent.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you can model company A with one equation.
that equation would be:
y = .85*x
y is the sale price.
x is the retail price.
you cannot model company B with one equation.
at least i haven't been able to.
it requires programmed logic and 2 equations to handle it.
the first equation does not apply any discount up to 20 dollars.
the second equation applies 20% discount if the value of the order is greater than 20 dollars.
the question then remains as to whether the discount is applied to the whole order or just to the part of the order that is greater than 20 dollars.
i'll assume the 20% discount only applies to the amount over the 20 dollars spent.
the equation for company B would be:
if the retail price is less than or equal to 20 dollars than:
y = x
if the retail price is greater than 20 dollars, then:
y = .80 * (x-20) + 20
here's a small table of the difference in cost to the customer.
retail price company A sale price company B sale price
0 0 0
20 17 20
40 34 36
60 51 52
80 68 68
100 85 84
looks like the cut-over point is when the retail price is 80 dollars.
we can find the cut-over price by formula.
for company A, S = .85x
for company B, S = .80(x-20) + 20
make .85x = .80(x-20) + 20 and you'll find the cut-over point.
expand this equation to get:
.85x = .80*x - .8*20 + 20 which becomes:
.85x = .80x - 16 + 20 which becomes:
.85x = .80x + 4
subtract .80x from both sides of the equation to get:
.05x = 4
divide both sides of the equation by .05 to get:
x = 4/.05
simplify this to get:
x = 80
that's the cut-over point when company B discount becomes better than company A discount.
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I need to know what the linear equation would be for the following word problem:
A teacher is given a $300 stipend for supplies. Company A offers a 15% discount, but Company B offers a 20% discount after the first $20 spent.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As the request is formulated in the post, it is given in a strange form.
In my view, a correct, reasonable question to ask is THIS :
Which option is more profitable/preferable for the teacher ?
Which option provides more money for him to buy more supplies ?
Below is my solution for this modified formulation.
The conditions of Company A, with the 15% discount, allow the teacher to buy supplies for equivalent of
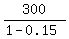 = = 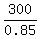 = 352.94 dollars, maximum.
The conditions of Company B allow the teacher to buy supplies for equivalent of
20 + = 352.94 dollars, maximum.
The conditions of Company B allow the teacher to buy supplies for equivalent of
20 + 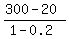 = 20 + = 20 +  = 20 + 350 = 370 dollars.
After getting these numbers, it becomes clear that option (B) is more profitable/preferable for the teacher. = 20 + 350 = 370 dollars.
After getting these numbers, it becomes clear that option (B) is more profitable/preferable for the teacher.
At this point, the problem is solved completely.
Here I not only solved/explained for you, but also created a nice brilliant meaningful problem
from this verbal semi-finished product, which you submitted in your post.
///////////////////////////////////////////////
OK, after thinking some time (several hours), I see now another way to treat your
problem and your request. Notice that the question itself is not formulated in your post,
so I should create it on my own, and it is the most complicated and most intelligent // ~ most delicate
part of creating right problem.
So, the question, which I propose, is THIS:
For each of the given options, write the functions describing the true cost before discounts
of supplies the teacher buys when he/she spends x dollars of $300 that he has.
The solution for this version is in two sections below.
(A) For company A, this true cost is a(x) = 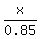 .
It says that when teacher spends x dollars, he/she actually buys supplies that cost
a(x) = .
It says that when teacher spends x dollars, he/she actually buys supplies that cost
a(x) = 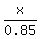 .
It accounts the given discount of 15%, provided by company A.
(B) For company B, when the teacher spends x dollars, he/she actually buys supplies that cost
/ = x, if x <= $20;
|
b(x) = (i will write it in two lines) = /
\
|
\ = 20 + .
It accounts the given discount of 15%, provided by company A.
(B) For company B, when the teacher spends x dollars, he/she actually buys supplies that cost
/ = x, if x <= $20;
|
b(x) = (i will write it in two lines) = /
\
|
\ = 20 + 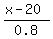 , if x > $20.
This awkward combination of sticks depicts the unification of two formulas into one. , if x > $20.
This awkward combination of sticks depicts the unification of two formulas into one.
These two formulas, one for a(x) in section (A) and the other for b(x) in section (B), are what you request
in your post, <---> in my interpretation.
|
|
|