SOLUTION: Hello My name is Yash Shah. I am doing summer course for Algebra II and I have a following question. If a satellite circles earth at an altitude of a = 22,300 miles, it's spe

Algebra ->  Trigonometry-basics -> SOLUTION: Hello My name is Yash Shah. I am doing summer course for Algebra II and I have a following question. If a satellite circles earth at an altitude of a = 22,300 miles, it's spe      Log On


   

Question 478787: Hello
My name is Yash Shah. I am doing summer course for Algebra II and I have a following question.
If a satellite circles earth at an altitude of a = 22,300 miles, it's speed is the same as rotational speed of an earth.
To an observer on the equator, satellite appears to be stationary.
Using r = 4000 miles as a radius of an earth, determine the % of the equator that is within the signal range of the satellite.
Can you please assist me to resolve this problem.
Thank you.
Found 2 solutions by Earlsdon, Theo:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Hi Yash Shah:
A diagram of the situation would be most helpful in solving this problem:
Draw a circle representing the earth's equator.
Draw a point somewhere outside of the circle to represent the orbiting satellite.
Draw a line connecting the satellite and the centre of the circle.
Draw a line from the satellite to the circumference of the circle so that the line is tangent to the circle.
Draw a line from the centre of the circle to the point of tangency (this is the radius of the circle).
Now you have a picture of a right triangle whose base is the radius of the circle and whose hypotenuse is the line from the centre of the circle to the satellite.
The length of the radius is 4000 miles while the length of the hypotenuse is radius (4000) plus the altitude of the orbiting satellite (22,300) for a total of 26300 miles.
The goal is to find the angle (angle A) between the triangle's base and hypotenuse.
Use the inverse cosine function:
A+=+Cos%5E%28-1%29%284000%2F26300%29
A+=+81.25degrees.
But, as you will see from the diagram, this view from the satellite would encompass only half of the visble equator, so double this angle to 162.5 degrees.
Now you need to find out how much of the circle's circumference is subtended by a central angle of 162.5 degrees.
Use the ratio of:
162.5%2F360+=+0.451399 Now multiply by 100 to get the percentage.
%280.451399%29%28100%29+=+45.1399 or 45.14%

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
If a satellite circles earth at an altitude of a = 22,300 miles, it's speed is the same as rotational speed of an earth.
To an observer on the equator, satellite appears to be stationary.
Using r = 4000 miles as a radius of an earth, determine the % of the equator that is within the signal range of the satellite.
-----
a picture of your situation is shown below:
below that is the explanation.
$$$$$
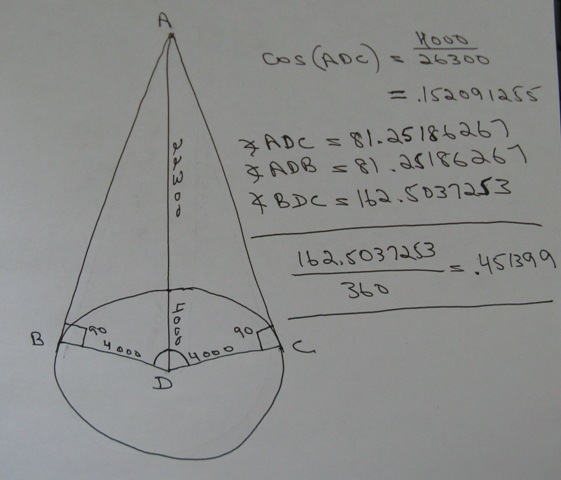
if the satellite appears stationary to an observer on the equator, then the orbit of the satellite must be along the equator because the earth revolves around the equator.
the picture shows the earth from a top down view so the equator looks like the circumference of the circle in the diagram.
the satellite is at point A.
the center of the earth is at point D.
if you draw a straight line from the satellite to the edge of the earth, that line will be a tangent to the circle.
the tangent to a circle is perpendicular to the radius of the circle at the point of tangency.
also, from an external point, the tangents to both sides of the circle are equal.
this means that:
AB is the same length of AC.
angle ABD and angle ACD are right angles (equal to 90 degrees).
BD and DC are radii of the circle and are each 4000 miles long.
the length of AD is equal to 22300 + 4000 = 26300 miles.
that's the distance from the satellite to the center of the earth which is also the center of the circle.
2 right triangles are formed.
they are:
triangle ABD and triangle ACD
the right angles of these triangles are angle ABD and angle ACD.
AD is the hypotenuse of each of these right triangles.
we need to find the central angles of the circle.
these are angle ADB and angle ADC.
these angles are equal to each other, so if we find 1 we will have found the other.
since these are right triangles, we can use trigonometry to find the angles.
we'll work with triangle ACD.
cosine (ADC) = adjacent / hypotenuse = DC/AD = 4000/26300 = .152091255
this means that angle ADC = 81.25186267
this means that angle ADB also equals 81.25186267 degrees because it is equal to angle ADC.
our central angle BDC is equal to the sum of angles ADB and ADC.
angle BDC = 162.5037253
since the circumference of the earth has a central angle of 360 degrees, then the percentage of the circumference of the earth represented by an angle of 162.5037253 is equal to 162.5037253/360 * 100% = 45.13992371%.
this rounds to 45.14% if you want to get to the nearest hundredth of a percent.
the circumference of the earth is given by the equation C = 2*pi*r where r is the radius.
this equates to 2*pi*4000 = 25,133 miles approximately.
the section of the circumference of the earth covered by the satellite signal would be equal to 45.14% of that which would make it equal to 11,345 miles approximately.