SOLUTION: ples please someone....I NEED HELP WITH THIS QUESTION I HAVE SUBMITTED IT SEVERAL TIMES THE FIRST TIME I DID NOT GIVE ALL OF THE INFORMATION, THE SECOND TIME I PUT IN THE WRONG EMA

Click here to see ALL problems on Probability-and-statistics

Question 478361: ples please someone....I NEED HELP WITH THIS QUESTION I HAVE SUBMITTED IT SEVERAL TIMES THE FIRST TIME I DID NOT GIVE ALL OF THE INFORMATION, THE SECOND TIME I PUT IN THE WRONG EMAIL ADDRESS....I DESPERATELY NEED HELP WITH IT I DO NOT KNOW WHERE TO BEGIN AND CAN NOT FIND AN EXAMPLE THAT CAN GUIDE ME ALONG THE WAY SO THAT I WILL EVEN KNOW WHERE TO BEGIN....PLEASE HELP!!!! LET X BE A RANDOM VARIABLE WITH THE FOLLOWING PROBAILITY DISTRIBUTION
X 0 1 2 3
P(X) 0.4 0.3 0.2 0.1

DOES X HAVE A BINOMIAL DISTRIBUTION JUSTIFY YOUR ANSWER
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
It doesn't look like it.
here's a reference on binomial distribuion
http://stattrek.com/tables/binomial.aspx#distribution
the binomial distribution approximates the normal distribution when the number of trials is large the the probability of success or failure is not extreme.
the normal distribution is a bell shaped curve where the mean is in the middle and 50% of the values are below the mean and 50% of the values are above the mean.
the binomial distribution is based on the binomial.
this reference has a calculator.
you enter the probability of success and the number of trials and the number of successes and then hit the return.
it will look like it went and did your calculations for you but it didn't.
you have to click on the calculate button before it does its thing.
perhaps you don't even need to hit the return.
try it, you'll see what i mean.
i believe that the binomial distribution stems from the binomial expansion formula.
here's a link that explains that.
http://www.regentsprep.org/Regents/math/algtrig/ATP4/bintheorem.htm
the formula for determining the probability of x out of n successes is:
p(x) =
s is the probability of success.
f is the probability of failure.
x is the number of successes.
n is the total number in the sample.
nCx is the combination formula for the number of ways to get x things out of n things.
example:
n = 10
x = 3
s = .2
f = 1-s = .8
p(3) = which becomes:
p(3) =
here's a table of data i created for this problem.
n = 10
x = 0 to 10
p(s) = .2
p(f) = .8

x p(x) 0 0.107374182 1 0.268435456 2 0.301989888 3 0.201326592 4 0.088080384 5 0.026424115 6 0.005505024 7 0.000786432 8 7.3728E-05 9 0.000004096 10 1.024E-07

here's a picture of the bar graph that was created from this data.

you can see that this bar graph approximates a normal distribution which is very similar to a binomial distribution.
any questions, write to dtheophilis@yahoo.com
hopefully this helps you understand better what the binomial distribution is and what it looks like.

Answer by ikleyn(52869)   (Show Source):
You can put this solution on YOUR website!
.
LET X BE A RANDOM VARIABLE WITH THE FOLLOWING PROBAILITY DISTRIBUTION

X 0 1 2 3 P(X) 0.4 0.3 0.2 0.1
DOES X HAVE A BINOMIAL DISTRIBUTION ? JUSTIFY YOUR ANSWER.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

        It is a good problem. It is good, because it is non-standard and is different from
        thousands other standard problems, that are usually offered in this area.

        Standard problems check if you know what is written in textbooks.
        Non-standard problems check, in addition, if you able to think independently,
        and motivate you to be creative.

        Tutor @Theo in his post wrote many words, but did not provide a direct solution.
        Meanwhile, the direct solution is simple, but requires to find and to apply some fresh idea.
        Therefore, it is educative and deserves your attention.

- - - S O L U T I O N - - - Let's for a minute that the distribution P(X) is a binomial. Then the number of trials is 3, and should be some probability 'p' such that P(i) = , i = 0, 1, 2, 3. (1) According to (1), for i = 0 should be P(0) = 0.4 = = = 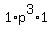. It implies p = 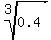= 0.7368063 (rounded). Next, according to (1), for i = 3 should be P(3) = 0.1 = = = 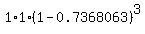= = 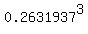0.018231671. Thus we got the : we got the number of 0.018231671 for P(3), different from the given value P(3) = 0.1. It that the given distribution is a binomial.

At this point, the problem is solved completely.