SOLUTION: What do you call this formula z=|z| (cosѲ + sinѲ)? And please tell more 'bout it.

You left out the i.  It's

z = |z|(cosѲ + i·sinѲ)

That's the trigonometric form of the complex number z = x + iy




The complex imaginary number z = x + yi is represented 
by the vector (line segment) from the origin to the point
(x,y).  So we draw and arbritrary point (x,y). (x,y) could 
be in any quadrant or even on an axis, but we'll draw it in 
the first quadrant. We'll label the length of the vector 
from the origin to the point (x,y) as |z|. 



Now from the point (x,y) we drop a perpendicular to the
x-axis (in green):


 
That makes a right triangle.  The base of that right triangle
is the same as the x-coordinate of the point (x,y), so it is x.
The green side of that right triangle
is the same as the y-coordinate of the point (x,y), so it is y.
The angle that the vector makes with the x-axis is labeled Ѳ.



So from the triangle,

 which gives 

and

 which gives 

Therefore



Then we can factor out the 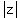 and get



That's the trigonometric or "trig" form of the complex 
number x+iy.

It allows us to bring trig into the algebra of complex
numbers.  It will make certain operations simpler. 

Edwin