Question 476358: Dear math teacher,
I am having difficulties with the following problem:
How many straight lines are determined by n points, no three of which lie in the same straight line?
Here is how I reasoned through the problem:
n = n
n = total number of points
3 = points that are NOT collinear
(n-3) = points that ARE collinear
"no three of which lie in the same straight line" means no three of n points lie in the same straight line; therefore,
A.) 3 points are NOT collinear and make nC3 = n!/((n-3)!3!)lines = n(n-1)(n-2)(n-3)!/(n-3)!3! = n(n-1)(n-2)/3! = n(n^2-3n+2)/3! = n^3-3n^2+2n/3! lines
B.) (n-3) points - are collinear points and make 1 line only. They are also points remaining from n points after the 3 points are selected in nC3 ways as in A.)
Total number of lines created from n points, no three of which lie in the same straight line = 1 line + n(n-1)(n-2)/3!; however, the textbook's answer is n(n-1)/2 lines.
Would you please correct me in this problem and explain to me what does "no three of which lie in the same straight line" truly mean?
Thank you very much for helping me figure this out.
Yours respectfully,
Ivanka
Found 2 solutions by MathLover1, richard1234:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
"no three of which lie in the same straight line" truly mean that a line is defined by two points;all you need is two points to draw a line through them. Through three points you can draw three lines (imagine triangle, extend its sides to make lines)
here are steps how to get a formula 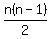 which is your answer which is your answer
1.
Draw, or suppose you have, n points in a plane. No three points lie in a straight line. You want to know how many lines can be drawn through two points at a time.
For example, you may have a circle with eight points, denoted A through H.
2.
Pick one point and determine how many pairs of points it can be in. If there are n points, the answer is n-1. This is how many lines can pass through that first point and another point at the same time.
Continuing with the above example, A can be matched up with B or C or D or E or F or G or H. That's seven possible matches.
3.
Pick the next point over. Its pairing with the first point has already been counted, but its pairing with the n-2 other points hasn't. Add n-2 to your earlier number, n-1, as possible lines through the points.
Continuing with the above example, B can have a line going through it and C through H. You don't count a line going through B and A, since you already did that in Step 2. So the possible lines through B are six.
4.
Continue with the pattern, adding n-3, then n-4, and so on. So the total sum of possible lines is n-1 + n-2 + n-3 + ... + 1. This is the same as summing up 1 + 2 + 3 + ... + n-1. It can be shown that the formula for 1 + 2 + 3 + ... + n-1 is:
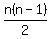
Continuing with the above example, there were eight points, so n=8 gives a total number of possible lines through the points of n(n-1)/2 = 8*7/2 = 28. You can verify this yourself by adding the 7 found in Step 2 to the 6 found in Step 3 to 5, 4, 3, 2 and 1 to get 28. It also matches the result discussed in the introduction where the number of points was  : :  possible lines. possible lines.
PS:
nadam se da je sada jasno Ivanka...:-)
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two points determine a unique line. You choose any two of these n points (order does not matter), so the number of lines is nC2 = n(n-1)/2. The phrase "no three which are collinear" means that no three points lie on the same line; this is good because you do not have to worry about overcounting lines.
|
|
|