Question 473829: The Fibonacci sequence is obtained as follows: The first number is 1, the second number is 1, and each number from the third and on is the sum of the previous 2. The first few terms are as follows: 1,1,2,3,5,8,13,.... Let A be the sum of the 2010 th term and the 2013 th term. Let B be the sum of the 2010 th term and the 2014 th term. What is the value of B/A? choose the answer and explain the reason to choose your response
8/5
3/2
5/3
2024/2023
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the 2010th term be x
Let the 2011th term be y
Let the 2012th term be z
Since A is the sum of the 2010th term and the 2013th term,
the 2013th term is A-x.
Since B is the sum of the 2010th term and the 2014th term,
the 2014th term is B-x.
So we have these five consecutive Fibonacci terms,
the 2010th, 2011th, 2012th, 2013th, and 2014th:
x, y, z, A-x, B-x
Every Fibonacci term after the 2nd is the sum of the two
preceding terms, so we have these three equations:
(1) z = x + y
(2) (A-x) = y + z
(3) (B-x) = z + (A-x)
From equation (2), which is
A - x = y + z
add x to both sides:
A = x + y + z
Subtract z from both sides
A - z = x + y
and by the equation (1):
z = x + y
So A - z = z since both equal to x + y
add z to both sides:
(4) A = 2z
Simplify (3)
(B-x) = z + (A-x)
B - x = z + A - x
Add x to both sides:
B = z + A
Multiply through by 2
2B = 2z + 2A
From equation (4), substitute A for 2z
2B = A + 2A
2B = 3A
Divide both sides by 2A
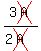
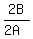 = = 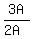
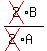 = = 
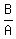 = =  Edwin
Edwin
|
|
|