Question 473678: If 1/x+1/y=1/4 and 1/x-1/y=3/4,then x=
(A)1/4
(B)1/2
(C)1
(D)2
(E)4
Thank you so much!
Found 3 solutions by Theo, MathTherapy, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the equations you have to work with are:
1/x + 1/y = 1/4 (first equation)
1/x - 1/y = 3/4 (second equation)
solve these 2 equations simultaneously to get your answer.
use the first equation to solve for 1/x.
1/x + 1/y = 1/4 becomes 1/x = 1/4 - 1/y
we can substitute for 1/x in the second equation to get:
1/x - 1/y = 3/4 becomes:
(1/4 - 1/y) - 1/y = 3/4
simplify this to get:
1/4 - 1/y - 1/y = 3/4
combine like terms to get:
1/4 - 2/y = 3/4
subtract 1/4 from both sides of this equation to get:
-2/y = 1/2
divide both sides of this equation by -2 to ge4t:
1/y = -1/4
now that we know what 1/y is equal to, we can solve for 1/x.
use the first equation of:
1/x + 1/y = 1/4
substitute -1/4 for 1/y to get:
1/x - 1/4 = 1/4
add 1/4 to both sides of this equation to get:
1/x = 1/2
you now have:
1/x = 1/2
1/y = -1/4
solve for x in the first of these 2 equations.
1/x = 1/2 is the equation.
multiply both sides of this equation by x to get:
|1 = x/2
multiply both sides of this equation by 2 to get:
2 = x which is the same as x = 2.
that's your answer.
selection D contains it.
similarly, we can solve for y to get y = -4
we have x = 2 and y = -4
substitute in your original equations to see that these solutions are good for both equations.
1/x + 1/y = 1/4 becomes 1/2 - 1/4 = 1/4 which is true.
1/x - 1/y = 3/4 becomes 1/2 + 1/4 = 3/4 which is also true.
Answer by MathTherapy(10556)  (Show Source):
Answer by ikleyn(52884)  (Show Source):
You can put this solution on YOUR website! .
If 1/x+1/y=1/4 and 1/x-1/y=3/4,then x=
(A)1/4
(B)1/2
(C)1
(D)2
(E)4
Thank you so much!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You have to solve this nice system of two non-linear equations
 +  =  , (1)
- =  . (2)
The standard method to solve it is to add these equations (adding both sides separately).
Doing this, the terms and 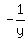 will annihilate, and you will get
+ = + ,
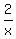 = 1,
2 = x.
Thus x = 2, and since the problem asks about 'x' only, the solution is just completed.
But for completeness, if you want to find 'y', substitute x=2 into equation (1)
 + = .
Simplify and find 'y'
= - =  =  ,
y = -4.
Thus you solved the system completely: x = 2, y = -4.
The answer to the problem's question is x = 2: option (D).
You may check the solution by substituting these found values of 'x' and 'y' in both equations.
It is a standard method solving such system of equations: short, straightforward and elegant.
It is also a standard method teaching for such problems.
Compare it with the many-lines solution by @Theo.
Happy learning ( ! )
|
|
|
