SOLUTION: [ab-5a+3b-15]/[ab-5a-2b+10] How would you simplify a fraction like this or like [2-x]/[x^2-4] VERY VERY VERY confusing and I've tried a few ways but they don't make much sense plea

What you need to practice doing is factoring by grouping,
factoring the difference of two squares, and how to rewrite
opposite differences.

 

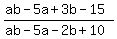First we need to factor the numerator and the denominator:

Factoring the numerator:

ab-5a+3b-15

Factor "a" out of the first two terms:

a(b-5)+3b-15

Factor "3" out of the last two terms:

a(b-5)+3(b-5)

Now we can factor (b-5) out of those two terms:

(b-5)(a+3)

Factoring the denominator:

ab-5a-2b+10

Factor "a" out of the first two terms:

a(b-5)-2b+10

Factor "-2" out of the last two terms:

a(b-5)-2(b-5)

Now we can factor (b-5) out of those two terms:

(b-5)(a-2)
  
So now 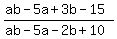 becomes



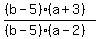Then we can cancel the (b-5)'s





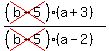
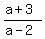That's the final answer.

-------------------------------



Rewrite the numerator:

2 - x , which is an opposite difference:

First write it in descending order

-x + 2

consider it as 

-1x + 2

Factor out -1, which causes the +2 to become -2

-1(x - 2)

Now factor the denominator x² - 4 as the difference of 
two perfect squares x² - 2² which factors as (x - 2)(x + 2)

So now  becomes



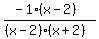Now you can cancel the (x-2)'s:



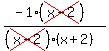And you end up with



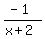You can leave it like that, or put the negative sign out front:



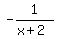Edwin