Question 473056: - 100 stones are placed on the ground 3 feet apart, the first being 3 feet from the basket and all of the stones are in a straight line, how far does a person travel who starts from the basket and bring the stone to it one by one? - did not match any documents.
Found 2 solutions by Theo, stanbon:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this looks a lot like an arithmetic sequence type of problem.
the last term in an arithmetic sequence is given by the formula:

the sum of the terms in an arithmetic sequence is given by the formula:

your arithmetic sequence of the stones is equal to:
3, 6, 9, 12, ........
the first stone is 3 feet from the basket.
each succeeding stone is 3 feet more than the preceding stone location from the basket.
when you retrieve these stone one by one, you have to travel twice the distance between stones because you have to travel to the stone and then you have to travel back.
your arithmetic sequence of the retrieval of the stones is equal to:
6, 12, 18, 24, ........
first we'll see if the formulas work.
then we'll use the formulas to solve your problem.
assume you only have 3 stones.
they are placed at 3, 6, 9 feet from the basket.
you walk 3 feet to the first stone, pick it up and walk 3 feet back to the basket.
you have walked 6 feet.
you now walk 6 feet to the second stone, pick it up and walk 6 feet back to the basket.
you have walked 12 feet to retrieve the second stone and walked 6 feet to retrieve the first stone for a total of 18 feet.
you now walk 9 feet to the third stone, pick it up and walk 9 feet back to the basket.
you have walked 18 feet to retrieve the third stone plus 12 feet to retrieve the second stone plus 6 feet to retrieve the first stone for a total of 18 + 12 + 6 = 36 feet.
to solve this using the formulas, our sequence will be:
6, 12, 18
those are the distances that have to be traveled to get to each stone and back.
the first term in the sequence is 6.
the last term in the sequence is given by the formula:

we replace a[1] with 6
we replace n-1 with 2
we replace d with 6
we get:
 which becomes a[n] = 18. which becomes a[n] = 18.
this is accurate so the formula to find the last term in the sequence works fine.
the sum of the terms in the sequence is given by the formula:

we replace n with 3
we replace a[1] with 6
we replace a[n] with 18
we get:
 which becomes: s[n] = 3*(24/2) which becomes s[n] = 3*12 = 36 which becomes: s[n] = 3*(24/2) which becomes s[n] = 3*12 = 36
this is accurate so the formula to find the sum of the terms in the sequence works fine as well.
36 is the total distance traveled to retrieve 3 stones.
we now apply the formulas to our problem.
our sequence is:
6, 12, 18, 24, 30, 36, ........a[n]
a[1] = 6
d = 6
n = 100
our formula of  becomes: becomes:
a[n] = 6 + (99)*6 = 600.
our formula of  becomes: becomes:
s[n] = 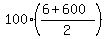 which becomes: which becomes:
s[n] = 100 * (303) which becomes:
s[n] = 30300.
you will have walked 30,300 feet to retrieve all 100 stones.
that's approximately 30,300 / 5280 = 5.7 miles.
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 100 stones are placed on the ground 3 feet apart, the first being 3 feet from the basket and all of the stones are in a straight line, how far does a person travel who starts from the basket and bring the stone to it one by one? - did not match any documents.
----
Procedure: Start with one stone; increase # of stones till you see a pattern.
1stone......3+3 ft = 2*3
2stone......(3+3)+(6+6)= 2*3+2*2*3
3stone......2*3+2*6+2*9
4stones.....2*3+2*6+2*9+2*12 = 2(1+2+3+4)3 = 6(1+2+3+4)
----
---
100stones....6(1+2+3...+100) 6*(100/2)(101) = 6*50*101 = 30300 ft.
====================
Cheers,
Stan H.
|
|
|