Question 472974: Find the maximum number of x-intercepts and the maximum number of turning points that the graph of the function can have.
f(x) = – x2 + x4 – x6 + 3
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Applying Descartes' rule of signs, the following are the possibilities for the distribution of roots (3 variations of sign):
(i) 3 positive, 3 negative roots, 0 complex
(ii) 3 positive, 1 negative roots, 2 complex
(iii) 1 positive, 3 negative roots, 2 complex
(iv) 1 positive, 1 negative roots, 4 complex
Since the polynomial is symmetric, cases (ii) and (iii) are eliminated.
Taking the derivative, we get  . Since the factor . Since the factor 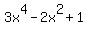 does not have real roots, there is only 1 turning point, and it happens at x = 0. This means that there are 2 x-intercepts. does not have real roots, there is only 1 turning point, and it happens at x = 0. This means that there are 2 x-intercepts.
We verify graphically:


|
|
|