Question 471935: Given that sin θ = -1/2 for an angle in Quadrant III, find the exact value of sec θ .
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given that the angle is in Quadrant III, it must be bigger than 180 degrees and less than 270 degrees. For angles in this quadrant the adjacent side is on the horizontal line that is the negative x-axis and the opposite side is a vertical line running below the x-axis in the negative (downward) direction.
.
Recall that relative to the sides of a right triangle the sine of an angle is defined as:
.

.
You are told that:
.

.
By comparing this equation to the previous equation that defines the sine, you can see that the the numerator is the opposite side in the definition and it is -1 in the sine that you were given. The hypotenuse is always positive, and is the denominator of 2. With those two sides now known, you can use the Pythagorean theorem to find the unknown third (adjacent) side. The Pythagorean theorem states that the square of the hypotenuse (h) equals the sum of the other two sides (opposite "o" and adjacent "a". In equation form this is:
.

.
The hypotenuse is 2 and the opposite side is (-1) so the Pythagorean theorem becomes:
.

.
Squaring the two terms out results in:
.

.
Subtract 1 from both sides to get:
.

.
and by taking the square root of both sides you get:
.

.
So now you know all three sides for this triangle. And you know the angle whose sine is -1/2 has an adjacent side equal to the square root of 3. You also know that relative to the sides of a right triangle the cosine is defined by the equation:
.

.
and you further know that for angles in Quadrant III the adjacent side is on the negative x axis and is, therefore, negative. So for the Quadrant III angle whose sine is -1/2, it cosine is:
.

.
and if you divide the square root of 3, which is 1.732050808, by 2 you get:
.

.
Finally, the secant of an angle is defined as being:
.

.
and you know that the cosine of this angle is -0.866025403, so this value can be substituted into this equation and you get:
.

.
Doing the division on the right side results in:
.

.
and that's the answer to this problem. The secant of the angle whose sine in the third quadrant is -1/2 is given by 
.
This is a geometrical way of doing the problem. You can also do it by using a calculator as follows.
.
You are given that the magnitude of the sine of an angle is 1/2 (or 0.5). Enter 0.5 into your calculator and calculate the arcsine of 1/2 (use the sin^(-1) key which is usually the "shift" key followed by the sin key). You will get 30 degrees as the answer. In Quadrant III this 30 degree angle becomes 180 degrees + 30 degrees more or 210 degrees. Now that you know the angle is 210 degrees, enter 210 on the calculator and press the "cos" key to get -0.866025403 as the value of the cosine. Then use the "1/x" key to invert this value (since 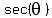 is the inversion of is the inversion of  ) and you have the answer of: ) and you have the answer of:
.

.
which is the same value that we got by determining the lengths of the sides and using those lengths to arrive and the cosine and then the secant.
.
I hope this isn't too confusing and that you develop a little better understanding of trigonometry by thinking your way through this problem.
|
|
|