|
Question 471413: The following is what I am looking for in describing a line. This is what is needed to describe a linear graph after graphing. This describes the graph without having the graph available.
The items needed: x intercept, y intercept, slope, slant, and the quadrants the line passes through when graphed..
Example: Graph 5x + 2y = 10. (Actually graph this and work through the steps as we go. Ask questions as needed.)
1. x intercept: Let y = 0, substitute in place of y and then solve for x: 5x = 10, x = 2.
2. y intercept: Let x = 0, substitute in place of x and then solve for y: 2y = 10, y = 5.
3. slope: Put into slope intercept form: Solve for y. Add -5x to each side to get 2y = -5x + 10. Now divide by 2 to solve for 1y: y = (-5x + 10) / 2 but each term can be put over 2 so we have y = (-5/2)x + 10/2 = (-5/2)x = 5 has form y = mx + b whre m = -5/2 for the slope. Note that we can also check our y intercept here since b should also be the y intercept. Glancing back, we found that we did get 5 above for the y intercept. This is just an additional safeguard.
4. Slant: If the slope is positive we slant to the right /, if the slope is 0 we are horizontal __, If the slope is undefined we are vertical |, but we have a slope that is negative and it will slant to the left. \.
5. Quadrants passing through: This line will pass through Q1, Q2, and QIV and will not enter QIII.
Note: Just describe the graphs. Give the five characteristics that I outlined above for each line graphed.
Your turn. Describe the graph of the linear equation: 3y – 2y = 18. Do so by first graphing it for yourself. Then list the five characteristics above in describing your graph and post in this thread.
Answer by Tatiana_Stebko(1539)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
1. x-intercept: Let  , substitute in place of , substitute in place of  and then solve for and then solve for  : :  , ,  , ,  . .
2. y-intercept: Let  , substitute in place of , substitute in place of  and then solve for and then solve for  : :  , ,  , , 
.
3. slope: Put into slope intercept form: Solve for  . Add . Add 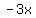 to each side to get to each side to get  . Now divide by (-2) to solve for . Now divide by (-2) to solve for  : :  but each term can be put over (-2) so we have but each term can be put over (-2) so we have  has form has form  whre whre  for the slope. for the slope.
4. Slant: If the slope is negative we slant to the left \, if the slope is 0 we are horizontal __, If the slope is undefined we are vertical |, but we have a slope that is positive and it will SLANT TO THE RIGHT /.
5. Quadrants passing through: This line will pass through Q1, QIII, and QIV and will not enter Q2.
|
|
|
| |